– Ndalo kërkimin! "Më në fund e kemi gjetur", bërtiti komisioneri MacCarnigan.
– Kujt zotëri? - pyeti togeri i dytë Pierron.
– Tek një prej të poshtërve më të pakapshëm që mund të imagjinoni ndonjëherë. Unë e kam kërkuar për gati 50 vjet.
– Nuk e kisha idenë, komisioner. Për kë bëhet fjalë?
– Numri i tij është Ein Stein dhe më është dashur pothuajse një jetë për ta gjetur.
- Për kë bëhet fjalë? A keni ndonjë foto të vetes atje?
– Po, e kam pikërisht këtu, kështu duket, por mos u gënjeni nga pamja e pafajshme, ky zotëri i vogël këtu na ka mbajtur pezull për gati dhjetë dekada.
MacCarnigan më pas i tregoi agjentit Pierron foton e Ein Stein, kjo foto:
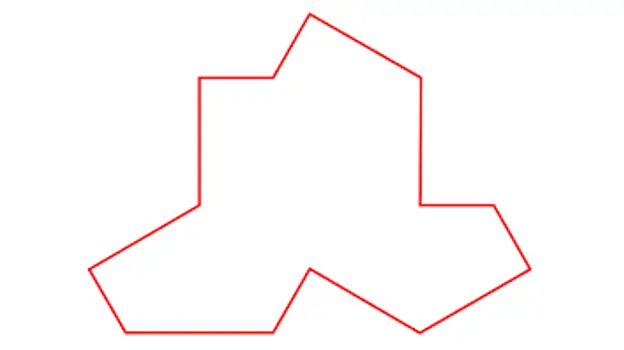
Në Stein.
Kjo histori e shkurtër policore mund të duket si një shaka, por nëse ndryshojmë detektivë për matematikanët, bëhet një nga zbulimet më të mrekullueshme matematikore që janë përjetuar vitet e fundit. Por për të kuptuar qëllimin e kësaj historie, fillimisht duhet të flasim për një nga fushat në të cilat shkrihen matematika dhe arti: mozaikët.
Gazetat Mozaik
Të gjithë kemi parë një mozaik në një moment të jetës sonë. Këto janë vepra të vogla artistike ose dekorative që bëhen duke përdorur pjesë të vogla që përshtaten së bashku.


Disa shembuj të mozaikëve
Kur flasim për mozaikët në matematikë, zakonisht i referohemi asaj që njihet si tesellations, që është një mënyrë për të rregulluar pjesët ose pllakat në mënyrë që këto pjesë të kenë skaje të përbashkëta dhe të mos lënë vrima.
Shumë kohë më parë, matematikanët i bënë vetes pyetjen e mëposhtme:
Me çfarë lloj copash mund ta përpunoj avionin?
Kjo është, çfarë lloj copash mund të përdor për këtë, duke i vendosur ato në mënyrë që pllakat të prekin anët e përbashkëta, të mos ketë boshllëqe në aeroplan. Është e qartë se rrathët nuk janë në këtë grup të përzgjedhur, pasi nëse dua të rrafshoj rrafshin duke përdorur vetëm rrathë, do të mbeten boshllëqe. Hajde, do të më duhet të vendos fino fikse.

Rrathët lënë boshllëqe
Megjithatë, ka shumë figura të tjera me të cilat mund ta përpunojmë rrafshin, si për shembull trekëndëshat, katrorët ose gjashtëkëndëshat.

Tessellation me një shumëkëndësh të vetëm të rregullt
Ose mund ta shtrojmë rrafshin me kombinime të këtyre ose figurave të tjera.

Tessellation me disa shumëkëndësha të rregullt
Ose mund ta bëni avionin edhe me kombinime më ekstravagante:
Tesselacione të tjera të mundshme
Por ai ka konsideruar larminë e madhe të teselave që ka paraqitur, të gjitha kanë diçka të përbashkët, pra janë periodike. Termi periodik i referohet faktit se ka ndonjë përkthim, përveç zeros, që e lë të gjithë mozaikun të njëjtë. Nga sa kuptojmë, është e barabartë me atë që nëse shtrojmë një sipërfaqe, qeramikojmë sytë dhe dikush lëviz të gjithë mozaikun në një drejtim të caktuar dhe më pas mbulon sytë përsëri, nuk do të jemi në gjendje të vlerësojmë ndryshimin midis mozaikut origjinal dhe atij të zhvendosur. një.
Mozaikë pa gazeta
Në ndryshim nga tesellacionet periodike gjejmë tesellacione jo periodike, të cilat janë ato për të cilat nuk ka asnjë përkthim, jo nul, që e lë mozaikun me të njëjtën pamje. Nuk është e vështirë të gjesh mozaikë jo periodikë, mjafton, për shembull, të marrim një tesel periodik, le të mendojmë për shembull një të formuar vetëm nga katrorë, dhe një katror të vetëm të të gjithë mozaikut e ndajmë në dy trekëndësha. Është e qartë se është ende një model i aeroplanit, por nuk do të ketë asnjë përkthim që e lë të gjithë teserën të njëjtë pasi ne do të jemi në gjendje të dallojmë midis mozaikut origjinal dhe atij të zhvendosur thjesht duke vëzhguar pozicionin e modifikuar të dy trekëndëshave.
Mozaikë aperiodikë
Por tani është kur gjërat bëhen interesante, sepse është kur shfaqet koncepti i mozaikut aperiodik, që janë ato që, duke qenë periodikë, nuk plotësojnë kushtin shtesë që të mos kenë rajone arbitrare të mëdha që janë periodike. Në të njëjtën mënyrë kjo ide mund të dëgjohet si në një mozaik aperiodik, nëse marrim një pjesë mjaft të madhe, ajo nuk përsëritet në pjesën tjetër të mozaikut. Sigurohuni që mostra e mozaikut që asnjë periodik nuk e përshkruan më parë të mos jetë periodike pasi mund të gjejmë rajone arbitrare të mëdha që janë periodike, thjesht merrni pjesë arbitrare të mëdha që nuk përfshijnë asnjë trekëndësh.
Pra, pyetja që lind natyrshëm është kjo:
A ka mozaikë periodikë?
Kjo pyetje, e cila filloi të diskutohej në gjysmën e dytë të shekullit të kaluar, shpejt mori një përgjigje pohuese dhe një nga të parët që gjeti një tesel aperiodik ishte Raphael M. Robinson. Mozaiku i përshkruar nga Robinson në 1971 ishte i përbërë nga 6 pllaka të njëpasnjëshme.

Pllaka Robinson
Disa vjet më vonë, gjithashtu në vitet 70, Roger Penrose mori dy pllaka aperiodike që mund të ndërtoheshin, secila duke përdorur vetëm dy pllaka të ndryshme. E para nga këto tekste është e përbërë nga dy rombe të ndryshëm:
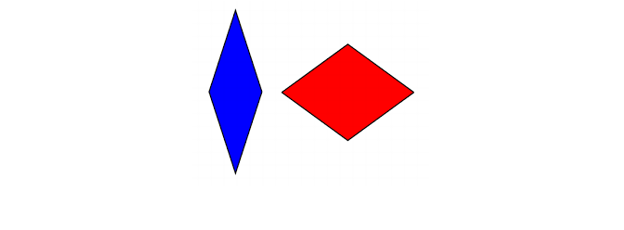
Tesserae penrose (rombe)
Ju mund të prodhoni mozaikë si të tillë:
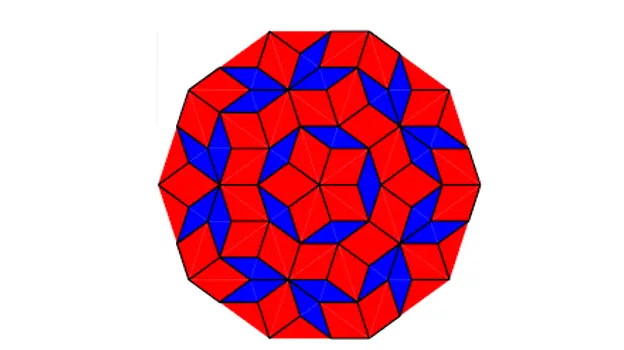
Mozaiku Penrose
E dyta nga këto teselacione aperiodike jepet nga dy pjesë të njohura si kometa dhe shigjeta, për arsye të dukshme:
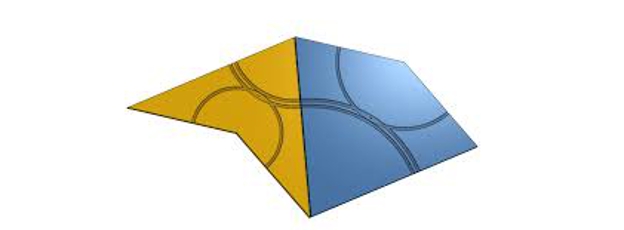
Penrose tesserae (qift dhe shigjetë)
Epo, ekziston pyetja që një shputar mund të jetë si më poshtë:
A ka mozaikë aperiodikë të përbërë nga një pllakë e vetme?
Ky problem është njohur si problemi i Ein Stein (nga gjermanishtja për "një gur") dhe për gati 50 vjet ka mbetur i pazgjidhur. Deri në marsin e kaluar!
Zbulimi i Ein Stein
Më 20 mars, shkencëtarët David Smith, Joseph Samuel Myers, Craig S. Kaplan dhe Chaim Goodman-Strauss nga Universitetet e Kembrixhit, Waterloo dhe Arkansas botuan veprën "Një monotile aperiodike" në të cilën ata përshkruan një formë të mundshme të një kërkimi të tillë. -pas pllakës që krijon një mozaik aperiodik me një pjesë unike.
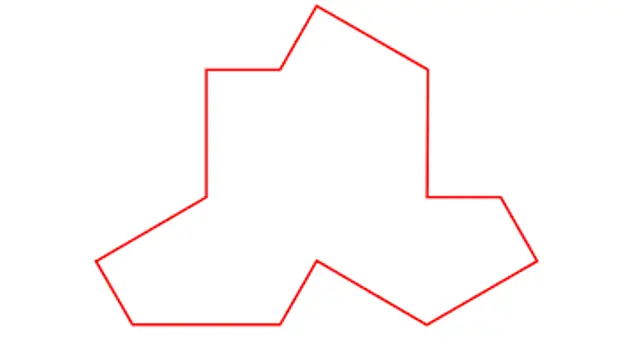
Pllakë e përshkruar nga Smith, Myers, Kaplan dhe Goodman-Strauss
Me këtë pllakë të vetme, e cila për mendimin tim duket shumë e ngjashme me një bluzë, tregon se mund të ndërtohen mozaikë aperiodikë si më poshtë:

Mozaik aperiodik i një pllake
Nëse jeni kurioz për këtë temë, mund të thelloheni në këtë zbulim në videon e mëposhtme:
në të cilën zbuluesit e saj flasin me njerëz të tjerë relevantë në zonë, duke përfshirë Çmimin Nobel në Fizikë Roger Penrose.
ABCdario de las Mathematics është një seksion që lind nga bashkëpunimi me Komisionin e Përhapjes së Shoqërisë Mbretërore Spanjolle Matematikore (RSME).
RRETH AUTORIT
Victor M. Manero

