- Itigil ang paghahanap! Nahanap na namin ito sa wakas,' bulalas ni Commissioner MacCarnigan.
- Sino sir? tanong ni Second Lieutenant Pierron.
"Sa isa sa mga pinaka madulas na rogue na maiisip mo. Halos 50 taon ko na itong hinahanap.
– Wala akong ideya, Commissioner. Tungkol kanino ito?
– Ang kanyang numero ay Ein Stein at inabot ako ng halos buong buhay upang mahanap ito.
- Tungkol kanino ito? May mga litrato ka ba diyan?
– Oo, mayroon ako dito, ito ang hitsura, ngunit huwag magpalinlang sa kanyang inosenteng hitsura, ang ginoo dito ay pinananatiling suspense sa amin sa halos sampung dekada.
Kaya ipinakita ni MacCarnigan kay Agent Pierron ang larawan ni Ein Stein, ang larawang ito:
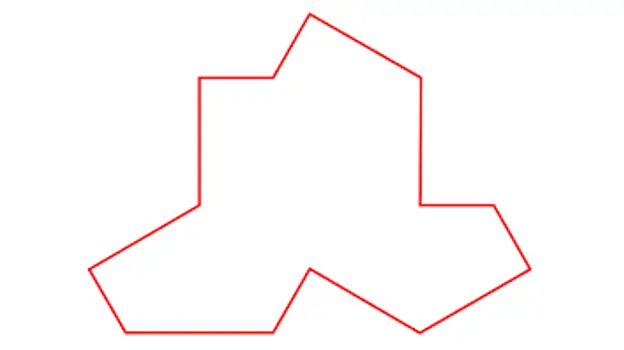
Sa Stein.
Ang maikling kasaysayan ng mga pulis ay maaaring mukhang isang biro, ngunit kung babaguhin natin ang mga detektib para sa mga mathematician, ito ay magiging isa sa mga pinakakahanga-hangang pagtuklas sa matematika na naganap sa mga nakaraang taon. Ngunit upang maunawaan ang saklaw ng kwentong ito, kailangan muna nating pag-usapan ang tungkol sa isa sa mga larangan kung saan pinagsama ang matematika at sining: mga mosaic.
mga mosaic na pahayagan
Lahat tayo ay nakakita ng isang mosaic sa isang punto sa ating buhay. Ang mga ito ay maliliit na masining o pandekorasyon na mga gawa na ginawa gamit ang maliliit na piraso na magkatugma.


Ilang halimbawa ng mosaic
Kapag pinag-uusapan natin ang tungkol sa mga mosaic sa matematika, karaniwang tinutukoy natin ang tinatawag na tessellations, na isang paraan ng pag-aayos ng mga piraso o tile upang ang mga piraso ay may mga karaniwang gilid at hindi nag-iiwan ng mga butas.
Isang mahabang panahon ang nakalipas mathematicians at matematika itinaas ang sumusunod na tanong
Anong uri ng mga piraso ang maaari kong i-tile ang eroplano?
Iyon ay, kung anong uri ng mga piraso ang maaari kong gamitin para doon, paglalagay ng mga ito upang ang mga tile ay magkadikit sa bawat isa sa mga karaniwang panig, walang mga puwang sa plano. Malinaw na ang mga bilog ay wala sa piling grupong ito, dahil kung gusto kong i-tile ang eroplano gamit lamang ang mga bilog ay iiwan nila ako ng mga butas. Halika, kailangan kong mag-cast ng nakapirming grawt.

ang mga bilog ay nag-iiwan ng mga puwang
Gayunpaman, mayroong maraming iba pang mga hugis kung saan maaari naming i-tile ang eroplano, tulad ng mga tatsulok, parisukat o hexagons.

Tessellation na may isang regular na polygon
O maaari naming i-tile ang eroplano na may mga kumbinasyon ng mga ito o iba pang mga figure.

Tessellation na may ilang regular na polygons
O maaari mo ring i-tile ang eroplano na may mas maraming mga kumbinasyon:
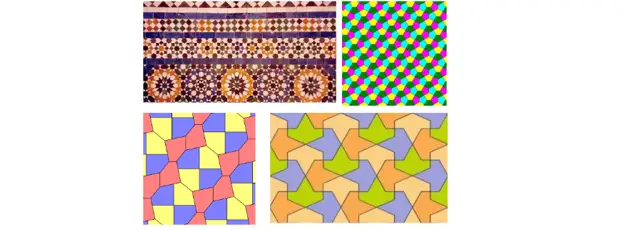
Iba pang posibleng mga tile
Ngunit pinag-isipan mo ang napakaraming iba't ibang mga tile na ipinakita mo, lahat sila ay may isang bagay na karaniwan, at iyon ay, ang mga ito ay pana-panahon. Ang terminong periodic ay tumutukoy sa katotohanan na mayroong ilang pagsasalin, maliban sa zero, na nag-iiwan sa buong mosaic na pareho. Mula sa aming naiintindihan, ito ay katumbas ng katotohanan na kung kami ay nag-tile ng isang ibabaw, ceramic ang mga mata at ang isang tao ay gumagalaw sa buong mosaic sa isang tiyak na direksyon at pagkatapos ay takip muli sa mga mata, hindi namin magagawang pahalagahan ang pagkakaiba sa pagitan ng orihinal na mosaic. at ang lumikas.
mosaic na walang pahayagan
Sa kaibahan sa mga pana-panahong pag-tile, makikita natin ang mga hindi pana-panahong mga tile, na kung saan walang pagsasalin, hindi zero, na nag-iiwan sa mosaic na may parehong hitsura. Hindi mahirap makahanap ng mga di-pana-panahong mosaic, sapat na, halimbawa, na kumuha ng pana-panahong pag-tile, isipin natin, halimbawa, ang isang nabuo lamang ng mga parisukat, at ang isang parisukat ng buong mosaic ay nahahati sa dalawang tatsulok. . Malinaw na ito ay isang tessellation pa rin ng eroplano, ngunit walang magiging anumang pagsasalin na mag-iiwan sa buong tesserae na pareho dahil magagawa nating makilala sa pagitan ng orihinal na mosaic at ang inilipat nito sa pamamagitan lamang ng pagmamasid sa binagong posisyon ng dalawang tatsulok.
aperiodic tiling
Ngunit ngayon ay kapag ang mga bagay ay nagiging kawili-wili, dahil ito ay kapag ang konsepto ng aperiodic mosaic ay lilitaw, na kung saan, habang hindi pana-panahon, ay nagbibigay-kasiyahan sa dagdag na kondisyon na wala silang arbitraryong malalaking rehiyon na pana-panahon. Sa parehong paraan ang ideyang ito ay maririnig tulad ng sa isang aperiodic mosaic, kung kukuha tayo ng sapat na malaking piraso, hindi ito mauulit sa natitirang bahagi ng mosaic. Siguraduhin na ang sample ng mosaic na walang periodical na naglalarawan dati ay hindi aperiodic dahil makakahanap tayo ng mga arbitraryong malalaking rehiyon na pana-panahon, kunin lang ang mga malalaking piraso na walang kasamang tatsulok.
Kaya, ang tanong na natural na lumitaw ay ang mga sumusunod:
Mayroon bang aperiodic mosaic?
Ang tanong na ito, na nagsimulang pag-aralan sa ikalawang kalahati ng huling siglo, ay nakatanggap ng isang positibong sagot at isa sa mga unang nakahanap ng aperiodic tessellation ay si Raphael M. Robinson. Ang mosaic na inilarawan ni Robinson noong 1971 ay binubuo ng 6 na magkakasunod na tesserae.

mga tile ng robinson
Pagkalipas ng ilang taon, noong 70s din, nakakuha si Roger Penrose ng dalawang aperiodic tile na maaaring itayo, bawat isa ay gumagamit lamang ng dalawang magkaibang tile. Ang una sa mga tessellation na ito ay nabuo ng dalawang magkaibang rhombus:
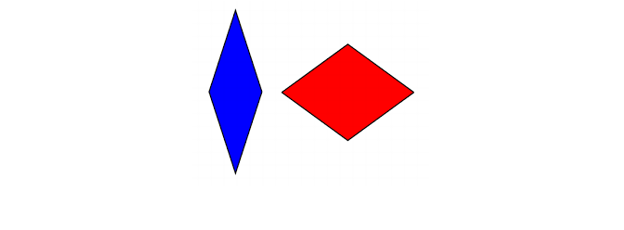
Penrose tile (rhombuses)
Maaari kang gumawa ng mga mosaic tulad ng:
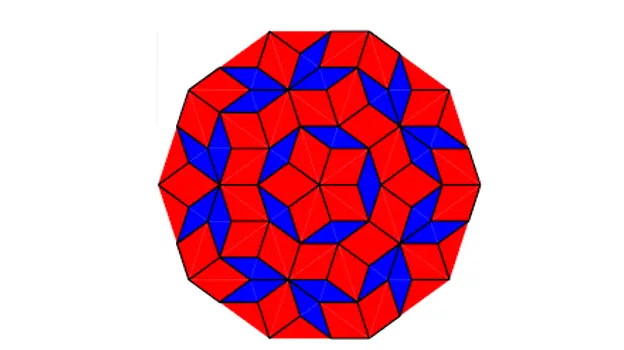
Pag-tile ng Penrose
Ang pangalawa sa mga aperiodic tiling na ito ay ibinibigay ng dalawang piraso na kilala bilang saranggola at arrow, para sa mga malinaw na dahilan:
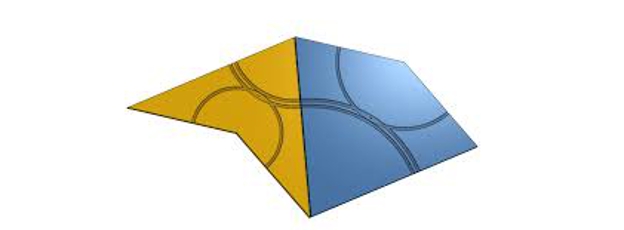
Penrose tile (kometa at arrow)
Well, may pagdududa na ang isang plantar ay maaaring ang mga sumusunod:
Mayroon bang mga aperiodic mosaic na nabuo ng isang tile?
Ang problemang ito ay kilala bilang ang problemang Ein Stein (mula sa Aleman para sa "isang bato") at sa halos 50 taon ito ay nanatiling hindi nalutas. Hanggang last March!
Ang pagtuklas ng Ein Stein
Noong Marso 20, inilathala ng mga siyentipiko na sina David Smith, Joseph Samuel Myers, Craig S. Kaplan at Chaim Goodman-Strauss mula sa Unibersidad ng Cambridge, Waterloo at Arkansas ang akdang 'An aperiodic monotile' kung saan inilarawan nila ang isang posibleng anyo ng isang mataas na hinahanap. pagkatapos ng tesserae na nagdudulot ng isang aperiodic mosaic na may kakaibang piraso.
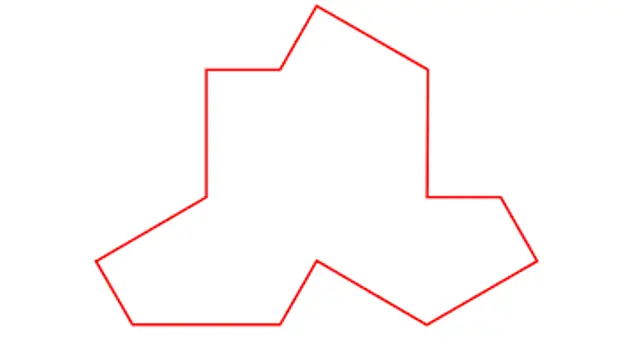
Tile na inilarawan nina Smith, Myers, Kaplan at Goodman-Strauss
Gamit ang nag-iisang tile na ito, na para sa akin ay halos kapareho sa isang T-shirt, ipinapakita niya na ang mga aperiodic mosaic na tulad ng sumusunod ay maaaring itayo:

Aperiodic mosaic ng isang tile
Kung ang iyong kuryusidad ay matino tungkol sa paksa, maaari mong suriin nang mas malalim ang pagtuklas na ito sa sumusunod na video,
kung saan ang mga nakatuklas nito ay nakikipag-usap sa iba pang nauugnay na tao sa lugar, kabilang ang Nobel Prize sa Physics na si Roger Penrose.
Ang ABCdario de las Matemáticas ay isang seksyon na nagmula sa pakikipagtulungan sa Dissemination Commission ng Royal Spanish Mathematical Society (RSME).
TUNGKOL SA AUTHOR
Victor M. Manero

