– ยุติการค้นหา! ในที่สุดเราก็พบมันแล้ว” ผู้บัญชาการแมคคาร์นิแกนอุทาน
- นายเป็นใคร? ถามร้อยตรีปิแอร์รอน
“ถึงหนึ่งในหัวไม้ที่ลื่นไหลที่สุดเท่าที่คุณจะจินตนาการได้ ฉันตามหามันมาเกือบ 50 ปีแล้ว
– ฉันไม่รู้เลย ผู้บัญชาการ มันเกี่ยวกับใคร?
- หมายเลขของเขาคือไอน์สไตน์ และฉันใช้เวลาเกือบทั้งชีวิตเพื่อค้นหามัน
- เกี่ยวกับใคร? คุณมีรูปถ่ายของคุณที่นั่นไหม?
– ใช่ ฉันมีมันอยู่ที่นี่ หน้าตาเป็นแบบนี้ แต่อย่าถูกหลอกด้วยรูปลักษณ์ที่ไร้เดียงสา สุภาพบุรุษคนนี้ทำให้เราใจจดใจจ่อมาเกือบสิบทศวรรษแล้ว
ดังนั้น MacCarnigan จึงแสดงให้เจ้าหน้าที่ Pierron ดูรูปถ่ายของ Ein Stein ภาพนี้:
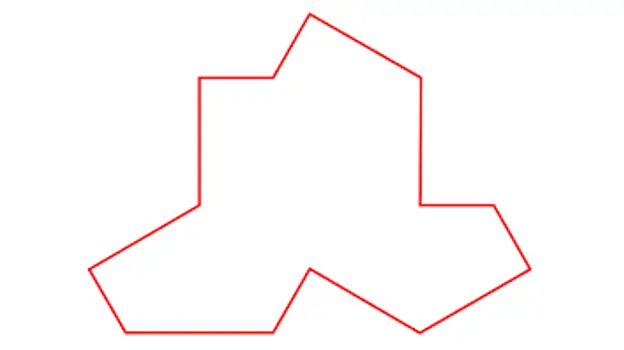
ในสไตน์.
ประวัติโดยย่อของเจ้าหน้าที่ตำรวจนี้อาจดูเหมือนเป็นเรื่องตลก แต่ถ้าเราเปลี่ยนนักสืบสำหรับนักคณิตศาสตร์ มันจะกลายเป็นหนึ่งในการค้นพบทางคณิตศาสตร์ที่ยอดเยี่ยมที่สุดที่เกิดขึ้นในช่วงไม่กี่ปีที่ผ่านมา แต่เพื่อให้เข้าใจขอบเขตของเรื่องนี้ ก่อนอื่นเราต้องพูดถึงหนึ่งในสาขาที่คณิตศาสตร์และศิลปะผสานกัน: โมเสก
หนังสือพิมพ์โมเสก
เราทุกคนเคยเห็นโมเสกในช่วงชีวิตของเรา เหล่านี้คืองานศิลปะหรืองานตกแต่งขนาดเล็กที่ทำขึ้นโดยใช้ชิ้นส่วนขนาดเล็กที่พอดีกัน


ตัวอย่างของโมเสค
เมื่อเราพูดถึงโมเสกในวิชาคณิตศาสตร์ เรามักจะอ้างถึงสิ่งที่เรียกว่าเทสเซลเลชัน ซึ่งเป็นวิธีการจัดเรียงชิ้นส่วนหรือกระเบื้องเพื่อให้ชิ้นส่วนเหล่านี้มีขอบเหมือนกันและไม่เหลือรู
นานมาแล้ว นักคณิตศาสตร์และนักคณิตศาสตร์ตั้งคำถามต่อไปนี้
ชิ้นส่วนประเภทใดที่ฉันสามารถใช้กระเบื้องระนาบได้?
นั่นคือฉันสามารถใช้ชิ้นส่วนประเภทใดได้บ้างโดยวางให้กระเบื้องสัมผัสกันในด้านทั่วไปไม่มีช่องว่างในระนาบ เห็นได้ชัดว่าวงกลมไม่ได้อยู่ในกลุ่มที่เลือกนี้ เนื่องจากถ้าฉันต้องการเรียงต่อกันเป็นระนาบโดยใช้วงกลมเท่านั้น พวกเขาจะปล่อยให้ฉันเป็นรู มาเลย ฉันจะต้องหล่อยาแนวถาวร

วงกลมเว้นช่องว่างไว้
อย่างไรก็ตาม มีรูปทรงอื่นๆ อีกมากมายที่เราสามารถเรียงต่อกันเป็นระนาบได้ เช่น สามเหลี่ยม สี่เหลี่ยม หรือหกเหลี่ยม

เทสเซลเลชันที่มีรูปหลายเหลี่ยมปกติรูปเดียว
หรือเราสามารถจัดเรียงระนาบด้วยการรวมกันของตัวเลขเหล่านี้หรือตัวเลขอื่น ๆ

Tessellation ที่มีรูปหลายเหลี่ยมปกติหลายรูป
หรือคุณสามารถเรียงต่อกันระนาบด้วยชุดค่าผสมที่หรูหรามากขึ้น:
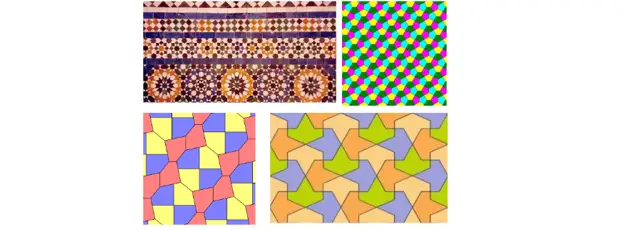
การปูกระเบื้องอื่นๆ ที่เป็นไปได้
แต่คุณได้ไตร่ตรองถึงความหลากหลายของการปูกระเบื้องที่คุณนำเสนอ พวกมันทั้งหมดมีบางอย่างที่เหมือนกัน และนั่นคือพวกมันเป็นระยะ คำว่าธาตุหมายถึงข้อเท็จจริงที่ว่ามีการแปลบางส่วน ที่ไม่ใช่ศูนย์ ซึ่งทำให้โมเสกทั้งหมดเหมือนกัน จากที่เราเข้าใจ ก็เปรียบได้กับข้อเท็จจริงที่ว่าถ้าเราปูกระเบื้องพื้นผิวเซรามิกที่ดวงตาแล้วมีคนขยับโมเสกทั้งหมดไปในทิศทางที่กำหนดแล้วปิดตาอีกครั้ง เราจะไม่สามารถเห็นความแตกต่างระหว่างโมเสกดั้งเดิมได้ และผู้พลัดถิ่น
กระเบื้องโมเสคที่ไม่มีหนังสือพิมพ์
ตรงกันข้ามกับการปูกระเบื้องเป็นระยะ เราพบการปูกระเบื้องแบบไม่เว้นระยะ ซึ่งเป็นการปูกระเบื้องที่ไม่มีการแปลหรือไม่มีศูนย์ ซึ่งทำให้ภาพโมเสกมีลักษณะเหมือนกัน การหากระเบื้องโมเสคที่ไม่ใช่เป็นระยะนั้นไม่ใช่เรื่องยาก ตัวอย่างเช่น การปูกระเบื้องเป็นระยะ ๆ ก็เพียงพอแล้ว ลองคิดดู เช่น หนึ่งเกิดจากสี่เหลี่ยมจัตุรัสเท่านั้น และสี่เหลี่ยมจัตุรัสเดียวของกระเบื้องโมเสคทั้งหมดจะแบ่งออกเป็นสองสามเหลี่ยม . เห็นได้ชัดว่ามันยังคงเป็นเทสเซลเลชันของระนาบ แต่จะไม่มีคำแปลใดที่จะทำให้เทสเซเรทั้งหมดเหมือนเดิม เนื่องจากเราจะสามารถแยกความแตกต่างระหว่างโมเสกดั้งเดิมกับโมเสกที่ถูกแทนที่ได้ง่ายๆ โดยสังเกตตำแหน่งที่แก้ไขของ สามเหลี่ยมสองอัน
ปูกระเบื้องเป็นระยะ
แต่ตอนนี้เป็นช่วงที่สิ่งต่าง ๆ น่าสนใจ เพราะเป็นช่วงที่แนวคิดของโมเสกแบบไม่มีคาบปรากฏขึ้น ซึ่งเป็นแบบที่ไม่เป็นไปตามเงื่อนไขพิเศษตรงที่ว่าไม่มีพื้นที่ขนาดใหญ่ตามอำเภอใจที่เป็นคาบ ในทำนองเดียวกันแนวคิดนี้สามารถได้ยินได้เช่นเดียวกับภาพโมเสกแบบไม่มีระยะ ถ้าเราใช้ชิ้นส่วนที่ใหญ่พอ จะไม่ทำซ้ำในส่วนที่เหลือของโมเสก ตรวจสอบให้แน่ใจว่าตัวอย่างโมเสกที่ไม่มีประจำเดือนอธิบายมาก่อนไม่ใช่แบบคาบ เนื่องจากเราสามารถหาพื้นที่ขนาดใหญ่ที่เป็นคาบได้ตามอำเภอใจ เพียงแค่ใช้ชิ้นส่วนขนาดใหญ่ตามอำเภอใจที่ไม่มีสามเหลี่ยมใดรูปหนึ่ง
ดังนั้น คำถามที่เกิดขึ้นตามธรรมชาติคือ:
มีกระเบื้องเคลือบสลับสีเป็นระยะหรือไม่?
คำถามนี้ซึ่งเริ่มศึกษาในช่วงครึ่งหลังของศตวรรษที่ผ่านมา ในไม่ช้าก็ได้รับคำตอบยืนยัน และ Raphael M. Robinson เป็นคนแรกๆ ที่ค้นพบเทสเซลเลชันแบบไม่มีคาบ โมเสกที่อธิบายโดยโรบินสันในปี พ.ศ. 1971 ประกอบด้วย tesserae 6 ตัวที่ต่อเนื่องกัน

กระเบื้องโรบินสัน
ไม่กี่ปีต่อมา ในช่วงทศวรรษ 70 โรเจอร์ เพนโรสได้กระเบื้อง aperiodic สองชิ้นที่สามารถสร้างได้ แต่ละชิ้นใช้กระเบื้องที่แตกต่างกันเพียงสองแผ่น เทสเซลเลชันอันแรกนี้เกิดจากสี่เหลี่ยมขนมเปียกปูนสองอันที่ต่างกัน:
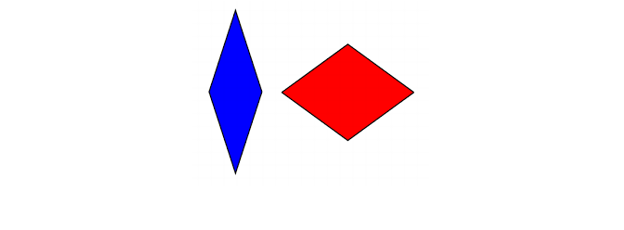
กระเบื้อง Penrose (รูปสี่เหลี่ยมขนมเปียกปูน)
คุณสามารถสร้างกระเบื้องโมเสคได้ดังนี้:
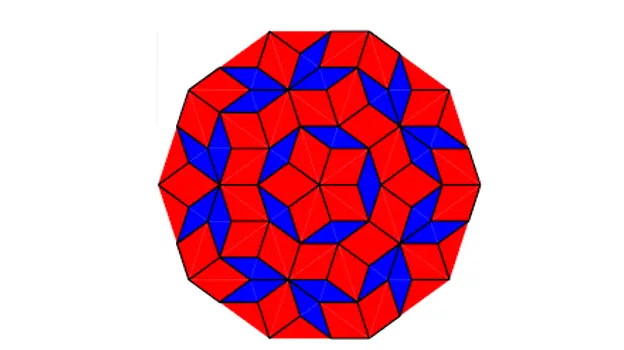
กระเบื้องเพนโรส
การปูกระเบื้องแบบ aperiodic ที่สองนี้มาจากสองชิ้นที่รู้จักกันในชื่อว่าวและลูกศร ด้วยเหตุผลที่ชัดเจน:
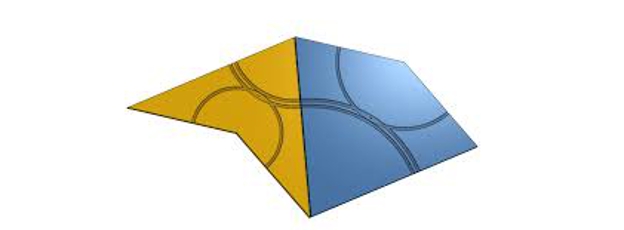
กระเบื้อง Penrose (ดาวหางและลูกศร)
มีข้อสงสัยว่าฝ่าเท้าอาจเป็นสิ่งต่อไปนี้:
มีกระเบื้องเคลือบสลับสีแบบ aperiodic ที่เกิดจากกระเบื้องแผ่นเดียวหรือไม่?
ปัญหานี้เป็นที่รู้จักกันในชื่อปัญหา Ein Stein (จากภาษาเยอรมันสำหรับ "a stone") และเป็นเวลาเกือบ 50 ปีแล้วที่ยังไม่ได้รับการแก้ไข ถึงเดือนมีนาคมที่ผ่านมา!
การค้นพบของไอน์สไตน์
เมื่อวันที่ 20 มีนาคม นักวิทยาศาสตร์ David Smith, Joseph Samuel Myers, Craig S. Kaplan และ Chaim Goodman-Strauss จากมหาวิทยาลัยเคมบริดจ์ วอเตอร์ลู และอาร์คันซอ ตีพิมพ์ผลงาน 'An aperiodic monotile' ซึ่งอธิบายรูปแบบที่เป็นไปได้ของ หลังจาก tesserae ที่ก่อให้เกิดกระเบื้องโมเสคเป็นระยะ ๆ ด้วยชิ้นส่วนที่ไม่เหมือนใคร
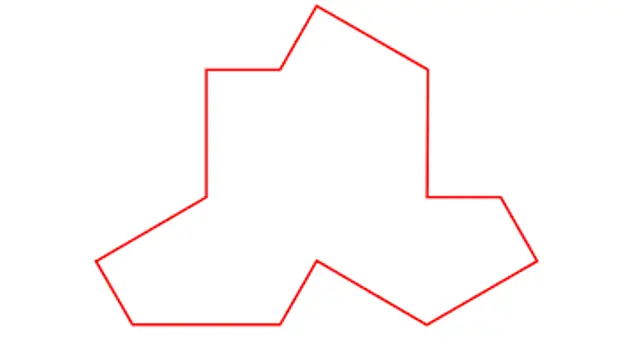
ไทล์บรรยายโดย Smith, Myers, Kaplan และ Goodman-Strauss
ด้วยกระเบื้องแผ่นเดียวนี้ ซึ่งสำหรับฉันแล้วดูเหมือนว่าจะคล้ายกับเสื้อยืดมาก เขาแสดงให้เห็นว่าสามารถสร้างกระเบื้องโมเสกแบบไม่มีระยะดังต่อไปนี้ได้:

โมเสกเป็นระยะของกระเบื้อง
หากความอยากรู้ของคุณยังไม่หมดไปเกี่ยวกับเรื่องนี้ คุณสามารถเจาะลึกลงไปในการค้นพบนี้ในวิดีโอต่อไปนี้
ซึ่งผู้ค้นพบได้พูดคุยกับบุคคลอื่นๆ ที่เกี่ยวข้องในพื้นที่ รวมทั้ง Roger Penrose ผู้ได้รับรางวัลโนเบลสาขาฟิสิกส์
ABCdario de las Matemáticas เป็นส่วนที่เกิดจากความร่วมมือกับ Dissemination Commission of the Royal Spanish Mathematical Society (RSME)
เกี่ยวกับผู้เขียน
วิคเตอร์ เอ็ม. มาเนโร

