– Stoppa sökandet! "Äntligen har vi hittat det", utbrast kommissionär MacCarnigan.
– Till vem sir? - frågade underlöjtnant Pierron.
– Till en av de mest svårfångade skurkar du någonsin kan föreställa dig. Jag har letat efter det i nästan 50 år.
– Jag hade ingen aning, herr kommissionsledamot. Vem handlar det om?
– Hans nummer är Ein Stein och det har tagit mig nästan en livstid att hitta honom.
- Vem handlar det om? Har du några bilder på dig själv där?
– Ja, jag har det här, så här ser det ut, men låt dig inte luras av dess oskyldiga utseende, den här lille herren här har hållit oss i spänning i nästan tio decennier.
MacCarnigan visade sedan agent Pierron fotot av Ein Stein, detta foto:
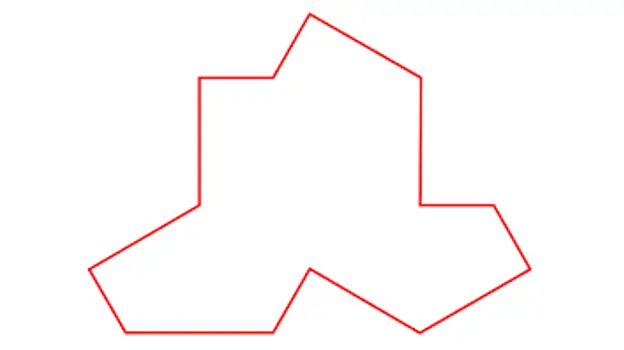
I Stein.
Den här korta polisberättelsen kan verka som ett skämt, men om vi byter deckare mot matematiker blir det en av de mest underbara matematiska upptäckterna som har upplevts de senaste åren. Men för att förstå omfattningen av denna berättelse måste vi först tala om ett av de områden där matematik och konst smälter samman: mosaik.
Mosaiktidningar
Vi har alla sett en mosaik någon gång i våra liv. Dessa är små konstnärliga eller dekorativa verk som är gjorda med små bitar som passar ihop.


Några exempel på mosaiker
När vi talar om mosaik i matematik hänvisar vi normalt till det som kallas tessellationer, vilket är ett sätt att ordna bitar eller brickor så att dessa bitar har gemensamma kanter och inte lämnar hål.
För länge sedan ställde matematiker sig själva följande fråga:
Vilken typ av bitar kan jag tesselera planet med?
Det vill säga vilken typ av bitar kan jag använda till det, placera dem så att brickorna berör gemensamma sidor, det finns inga luckor i planet. Cirklarna är uppenbarligen inte i denna utvalda grupp, eftersom om jag vill lägga till plattan på planet med enbart cirklar kommer det att finnas luckor kvar. Kom igen, jag måste lägga fast injekteringsbruk.

Cirklar lämnar luckor
Det finns dock många andra figurer som vi kan tesselera planet med, som till exempel trianglar, kvadrater eller hexagoner.

Tessellation med en enda vanlig polygon
Eller så kan vi kakla planet med kombinationer av dessa eller andra figurer.

Tessellation med flera regelbundna polygoner
Eller så kan du till och med pilla planet med mer extravaganta kombinationer:
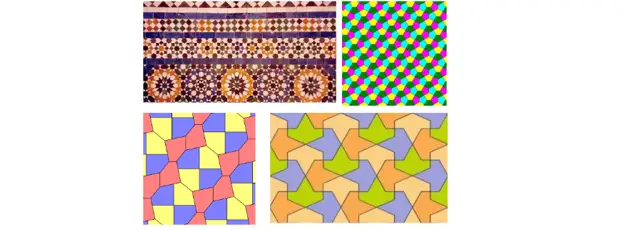
Andra möjliga tesselleringar
Men han har övervägt den stora variationen av tesseller som han har presenterat, alla har något gemensamt, och det vill säga att de är periodiska. Termen periodisk syftar på det faktum att det finns någon översättning, annan än noll, som lämnar hela mosaiken densamma. Vad vi förstår motsvarar det att om vi kaklar en yta, keramikerar ögonen och någon flyttar hela mosaiken i en specifik riktning och sedan täcker ögonen igen kommer vi inte att kunna uppskatta skillnaden mellan den ursprungliga mosaiken och den fördrivna ett.
Mosaiker utan tidningar
I motsats till periodiska tessellationer hittar vi icke-periodiska tessellationer, som är de för vilka det inte finns någon översättning, inte null, som lämnar mosaiken med samma utseende. Det är inte svårt att hitta icke-periodiska mosaiker, det räcker till exempel att ta en periodisk tessellation, låt oss till exempel tänka en som bara bildas av kvadrater, och vi delar en enda kvadrat av hela mosaiken i två trianglar. Uppenbarligen är det fortfarande en tessellation av planet, men det kommer inte att finnas någon översättning som lämnar hela tesseran densamma eftersom vi kommer att kunna skilja mellan den ursprungliga mosaiken och dess förskjutna genom att helt enkelt observera den modifierade positionen för de två trianglarna.
Aperiodiska mosaiker
Men nu är det när saker och ting blir intressanta, för det är när begreppet aperiodisk mosaik dyker upp, vilket är de som, eftersom de är periodiska, inte uppfyller det extra villkoret att de inte har godtyckligt stora regioner som är periodiska. På samma sätt kan denna idé höras som i en aperiodisk mosaik, om vi tar en tillräckligt stor bit, upprepas den inte i resten av mosaiken. Se till att mosaikprovet som ingen tidskrift beskriver tidigare inte är aperiodiskt eftersom vi kan hitta godtyckligt stora regioner som är periodiska, ta bara godtyckligt stora bitar som inte inkluderar någon av triangeln.
Så frågan som uppstår naturligt är denna:
Finns det aperiodiska mosaiker?
Denna fråga, som började diskuteras under andra hälften av förra seklet, fick snart ett jakande svar och en av de första som hittade en aperiodisk tessellation var Raphael M. Robinson. Mosaiken som beskrevs av Robinson 1971 bestod av 6 på varandra följande brickor.

Robinson kakel
Några år senare, också på 70-talet, fick Roger Penrose två aperiodiska plattor som kunde konstrueras, var och en med bara två olika plattor. Den första av dessa tesseller består av två olika romber:
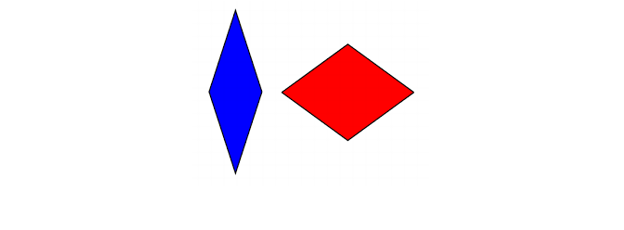
Penrose tesserae (rombussar)
Du kan producera mosaik som sådan:
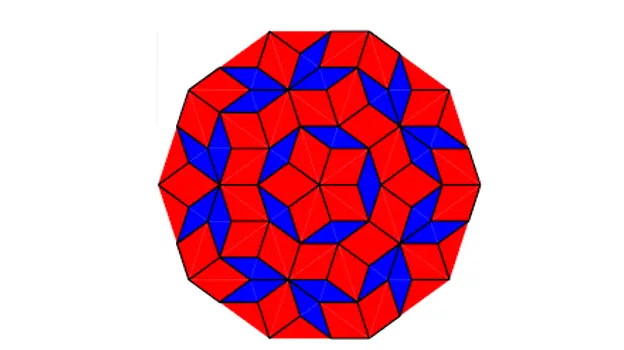
Penrose mosaik
Den andra av dessa aperiodiska tesselleringar ges av två delar som kallas kometen och pilen, av uppenbara skäl:
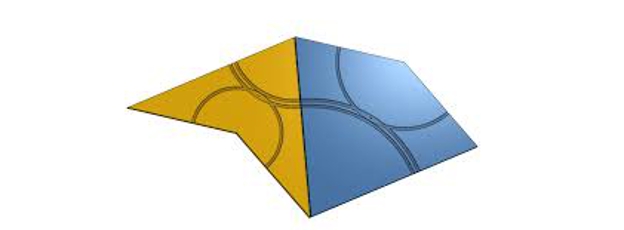
Penrose tesserae (drake och pil)
Tja, det finns frågan om att en plantar kan vara som följer:
Finns det aperiodiska mosaiker som består av en enda platta?
Detta problem har varit känt som Ein Stein-problemet (från tyskan för "en sten") och i nästan 50 år har det förblivit olöst. Tills i mars förra året!
Upptäckten av Ein Stein
Den 20 mars publicerade forskarna David Smith, Joseph Samuel Myers, Craig S. Kaplan och Chaim Goodman-Strauss från universiteten i Cambridge, Waterloo och Arkansas verket "An aperiodic monotile" där de beskrev en möjlig form av en sådan eftersökt -efter kakel som ger upphov till en aperiodisk mosaik med en unik bit.
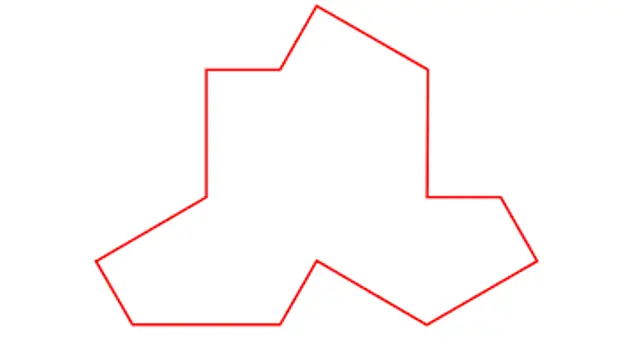
Kakel beskriven av Smith, Myers, Kaplan och Goodman-Strauss
Med denna enda kakel, som enligt min mening ser väldigt lik en T-shirt, visar det att aperiodiska mosaiker som följande kan byggas:

Aperiodisk mosaik av en kakel
Om du är nyfiken på ämnet kan du fördjupa dig i denna upptäckt i följande video,
där dess upptäckare talar med andra relevanta personer i området, inklusive Nobelpriset i fysik Roger Penrose.
ABCdario de las Mathematics är en sektion som uppstår genom samarbetet med Spridningskommissionen för Royal Spanish Mathematical Society (RSME).
OM FÖRFATTAREN
Victor M. Manero

