– Opriți căutarea! „În sfârșit am găsit-o”, a exclamat comisarul MacCarnigan.
— La cine domnule? -a întrebat sublocotenentul Pierron.
– Pentru unul dintre cei mai evazivi ticăloși pe care i-ai putea imagina vreodată. Îl caut de aproape 50 de ani.
– Habar n-aveam, domnule comisar. Despre cine este vorba?
– Numărul lui este Ein Stein și mi-a luat aproape o viață să-l găsesc.
- Despre cine este vorba? Ai vreo fotografie cu tine acolo?
– Da, îl am chiar aici, așa arată, dar nu vă lăsați păcăliți de aspectul ei inocent, acest mic domn de aici ne ține în suspans de aproape zece decenii.
MacCarnigan i-a arătat apoi agentului Pierron fotografia lui Ein Stein, această fotografie:
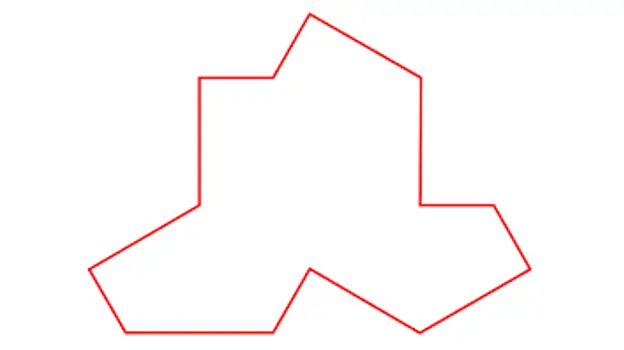
În Stein.
Această scurtă poveste polițistă poate părea o glumă, dar dacă schimbăm detectivii cu matematicieni, devine una dintre cele mai minunate descoperiri matematice care au fost experimentate în ultimii ani. Dar pentru a înțelege amploarea acestei povești trebuie mai întâi să vorbim despre unul dintre domeniile în care matematica și arta se îmbină: mozaicuri.
Ziare Mozaic
Cu toții am văzut un mozaic la un moment dat în viața noastră. Acestea sunt mici lucrări artistice sau decorative care sunt realizate folosind piese mici care se potrivesc între ele.


Câteva exemple de mozaicuri
Când vorbim despre mozaicuri în matematică, în mod normal ne referim la ceea ce se numește teselații, care este o modalitate de aranjare a pieselor sau plăcilor astfel încât aceste piese să aibă margini comune și să nu lase găuri.
Cu mult timp în urmă, matematicienii și-au pus următoarea întrebare:
Cu ce tip de piese pot tesela avionul?
Adică ce tip de piese pot folosi pentru asta, așezându-le astfel încât plăcile să atingă părțile comune, să nu existe goluri în plan. În mod clar, cercurile nu sunt în acest grup selectat, deoarece dacă vreau să plac planul folosind doar cercuri, vor rămâne goluri. Haide, va trebui să pun chit fix.

Cercurile lasă goluri
Cu toate acestea, există multe alte figuri cu care putem tesela planul, cum ar fi, de exemplu, triunghiuri, pătrate sau hexagoane.

Teselare cu un singur poligon regulat
Sau putem placa planul cu combinații ale acestor sau alte figuri.

Teselație cu mai multe poligoane regulate
Sau poți chiar să teselate avionul cu combinații mai extravagante:
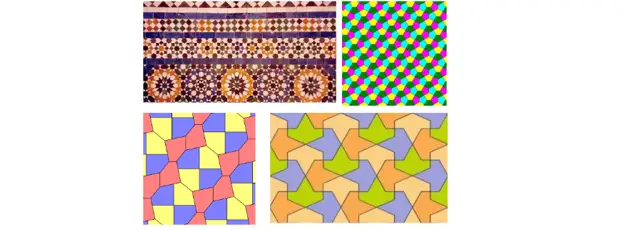
Alte teselații posibile
Dar a luat în considerare marea varietate de teselații pe care le-a prezentat, toate au ceva în comun, adică sunt periodice. Termenul periodic se referă la faptul că există o traducere, alta decât zero, care lasă tot mozaicul la fel. Din câte înțelegem, este echivalent cu faptul că dacă plăcem o suprafață, ceramică ochii și cineva mișcă întregul mozaic într-o direcție anume și apoi acoperă din nou ochii, nu vom putea aprecia diferența dintre mozaicul original și cel deplasat. unu.
Mozaice fără ziare
Spre deosebire de teselațiile periodice găsim teselații neperiodice, care sunt acelea pentru care nu există translație, nu nulă, care lasă mozaicul cu același aspect. Nu este greu de găsit mozaicuri neperiodice, este suficient, de exemplu, să luăm o teselație periodică, să ne gândim de exemplu la una formată doar din pătrate, și împărțim un singur pătrat din întregul mozaic în două triunghiuri. În mod clar, este încă o teselație a planului, dar nu va exista nicio translație care să lase întreaga teseră la fel, deoarece vom putea distinge între mozaicul original și cel deplasat prin simpla observare a poziției modificate a celor două triunghiuri.
Mozaicuri aperiodice
Dar acum este când lucrurile devin interesante, pentru că este atunci când apare conceptul de mozaic aperiodic, care sunt acelea care, fiind periodice, nu îndeplinesc condiția în plus ca să nu aibă regiuni arbitrar de mari care să fie periodice. La fel se aude această idee ca într-un mozaic aperiodic, dacă luăm o bucată suficient de mare, nu se repetă în restul mozaicului. Asigurați-vă că eșantionul de mozaic pe care nici un periodic nu îl descrie înainte nu este aperiodic, deoarece putem găsi regiuni arbitrar mari care sunt periodice, luați doar bucăți arbitrar mari care nu includ niciun triunghi.
Deci întrebarea care apare în mod natural este următoarea:
Există mozaicuri aperiodice?
Această întrebare, care a început să fie discutată în a doua jumătate a secolului trecut, a primit curând un răspuns afirmativ și unul dintre primii care au găsit o teselație aperiodică a fost Raphael M. Robinson. Mozaicul descris de Robinson în 1971 era alcătuit din 6 plăci succesive.

gresie Robinson
Câțiva ani mai târziu, tot în anii 70, Roger Penrose a obținut două plăci aperiodice care puteau fi construite, fiecare folosind doar două plăci diferite. Prima dintre aceste teselații este alcătuită din două romburi diferite:
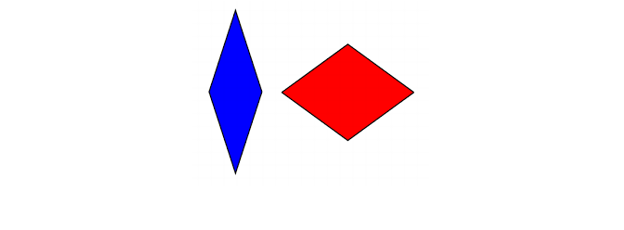
Teserae de Penrose (rombi)
Puteți produce mozaicuri ca atare:
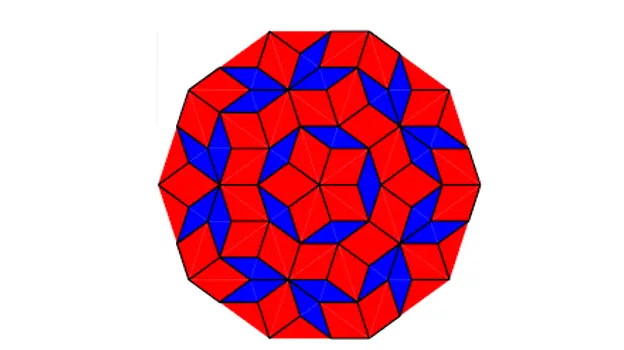
Mozaic Penrose
A doua dintre aceste teselații aperiodice este dată de două piese cunoscute sub numele de cometă și săgeată, din motive evidente:
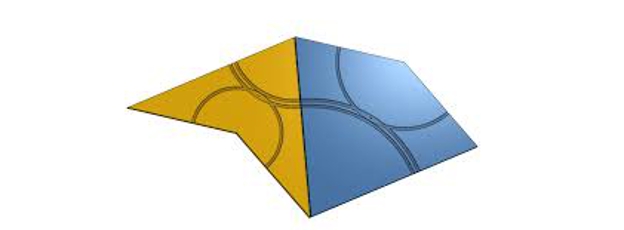
Teserae Penrose (zmeu și săgeată)
Ei bine, există întrebarea că un plantar ar putea fi după cum urmează:
Există mozaicuri aperiodice formate dintr-o singură plăci?
Această problemă a fost cunoscută sub numele de problema Ein Stein (din germană pentru „o piatră”) și timp de aproape 50 de ani a rămas nerezolvată. Până în martie trecut!
Descoperirea lui Ein Stein
Pe 20 martie, oamenii de știință David Smith, Joseph Samuel Myers, Craig S. Kaplan și Chaim Goodman-Strauss de la Universitățile din Cambridge, Waterloo și Arkansas au publicat lucrarea „An aperiodic monotile” în care au descris o posibilă formă a unui astfel de căutat. -after tigla care da nastere unui mozaic aperiodic cu o piesa unica.
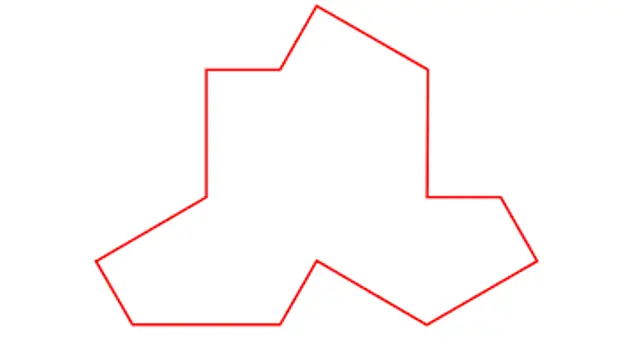
Tila descrisă de Smith, Myers, Kaplan și Goodman-Strauss
Cu această placă unică, care în opinia mea arată foarte asemănătoare cu un tricou, arată că pot fi construite mozaicuri aperiodice precum următorul:

Mozaic aperiodic al unei plăci
Dacă sunteți curios în legătură cu subiectul, puteți aprofunda această descoperire în următorul videoclip,
în care descoperitorii săi vorbesc cu alte persoane relevante din zonă, inclusiv cu Premiul Nobel pentru Fizică Roger Penrose.
ABCdario de las Mathematics este o secțiune care provine din colaborarea cu Comisia de Diseminare a Societății Regale Spaniole de Matematică (RSME).
DESPRE AUTOR
Victor M. Manero

