– Stopp letingen! Vi har endelig funnet det,» utbrøt kommissær MacCarnigan.
– Hvem sir? spurte sekondløytnant Pierron.
"Til en av de mest glatte skurkene du noen gang kan forestille deg. Jeg har lett etter den i nesten 50 år.
– Jeg ante ikke, kommissær. Hvem handler det om?
– Nummeret hans er Ein Stein, og det har tatt meg nesten et helt liv å finne det.
– Hvem handler det om? Har du noen bilder av deg der ute?
– Ja, jeg har det her, slik ser det ut, men ikke la deg lure av dets uskyldige utseende, denne herren her har holdt oss i spenning i nesten ti tiår.
Så MacCarnigan viste agent Pierron bildet av Ein Stein, dette bildet:
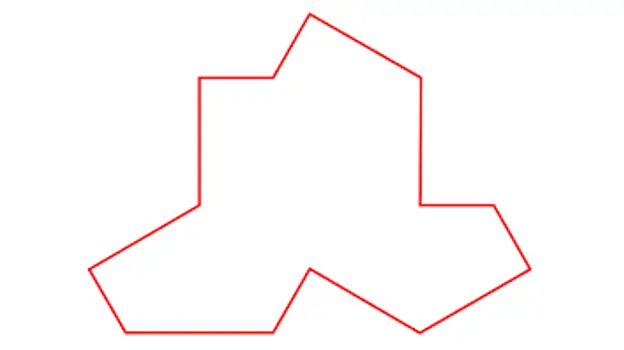
I Stein.
Denne korte historien om politimenn kan virke som en spøk, men hvis vi bytter detektiver for matematikere, blir det en av de mest fantastiske matematiske oppdagelsene som har skjedd de siste årene. Men for å forstå omfanget av denne historien, må vi først snakke om et av feltene der matematikk og kunst smelter sammen: mosaikk.
mosaikkaviser
Vi har alle sett en mosaikk på et tidspunkt i livet vårt. Dette er små kunstneriske eller dekorative verk som er laget ved hjelp av små biter som passer sammen.


Noen eksempler på mosaikk
Når vi snakker om mosaikk i matematikk, refererer vi vanligvis til det som kalles tessellasjoner, som er en måte å ordne brikker eller fliser på slik at disse bitene har felles kanter og ikke etterlater hull.
For lenge siden reiste matematikere og matematikere følgende spørsmål
Hva slags deler kan jeg flislegge flyet med?
Det vil si, hvilken type brikker kan jeg bruke til det, plassere dem slik at flisene berører hverandre på felles sider, det er ingen hull i planet. Det er klart at sirklene ikke er i denne utvalgte gruppen, siden hvis jeg vil flislegge flyet med bare sirkler, vil de etterlate meg med hull. Kom igjen, jeg må støpe fast fugemasse.

sirkler etterlater hull
Imidlertid er det mange andre former vi kan flislegge planet med, for eksempel trekanter, firkanter eller sekskanter.

Tessellasjon med en enkelt regulær polygon
Eller vi kan flislegge flyet med kombinasjoner av disse eller andre figurer.

Tessellasjon med flere regulære polygoner
Eller du kan til og med flislegge flyet med mer ekstravagante kombinasjoner:
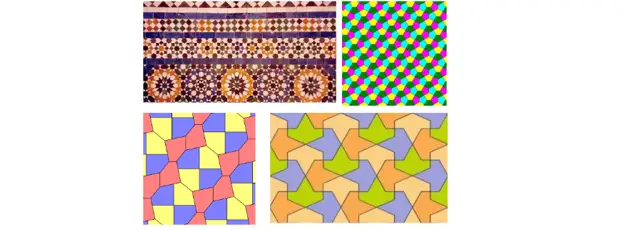
Andre mulige fliser
Men du har grublet over den store variasjonen av flislegging som du har presentert, de har alle noe til felles, og det vil si at de er periodiske. Begrepet periodisk refererer til det faktum at det er en eller annen oversettelse, annet enn null, som etterlater hele mosaikken den samme. Etter hva vi forstår, tilsvarer det det faktum at hvis vi fliser en overflate, keramiske øynene og noen beveger hele mosaikken i en bestemt retning og deretter dekker øynene igjen, vil vi ikke kunne forstå forskjellen mellom den originale mosaikken og den fordrevne.
mosaikk uten aviser
I motsetning til periodiske flislegginger finner vi ikke-periodiske flislegginger, som er de som det ikke er noen oversettelse for, ikke null, som etterlater mosaikken med samme utseende. Det er ikke vanskelig å finne ikke-periodiske mosaikker, det er nok, for eksempel å ta en periodisk flislegging, la oss for eksempel tenke en som bare er dannet av firkanter, og en enkelt firkant av hele mosaikken er delt inn i to trekanter . Det er klart at det fortsatt er en tessellasjon av flyet, men det kommer ikke til å være noen oversettelse som vil forlate hele tesseraene, siden vi vil være i stand til å skille mellom den originale mosaikken og dens forskjøvede enkelt ved å observere den modifiserte posisjonen til to trekanter.
aperiodisk flislegging
Men det er nå ting blir interessant, fordi det er når konseptet med aperiodisk mosaikk dukker opp, som er de som, selv om de ikke er periodiske, tilfredsstiller den ekstra betingelsen at de ikke har vilkårlig store regioner som er periodiske. På samme måte kan denne ideen høres som i en aperiodisk mosaikk, hvis vi tar et stort nok stykke, gjentar den seg ikke i resten av mosaikken. Pass på at mosaikkprøven som ingen tidsskrift beskriver tidligere ikke er aperiodisk siden vi kan finne vilkårlig store områder som er periodiske, bare ta vilkårlig store biter som ikke inkluderer noen av trekantene.
Så spørsmålet som naturlig dukker opp er følgende:
Finnes det aperiodiske mosaikker?
Dette spørsmålet, som begynte å bli studert i andre halvdel av forrige århundre, fikk snart et bekreftende svar, og en av de første som fant en aperiodisk tessellasjon var Raphael M. Robinson. Mosaikken beskrevet av Robinson i 1971 besto av 6 påfølgende tesseraer.

robinson fliser
Noen år senere, også på 70-tallet, skaffet Roger Penrose to aperiodiske fliser som kunne bygges, hver med kun to forskjellige fliser. Den første av disse tessellene er dannet av to forskjellige romber:
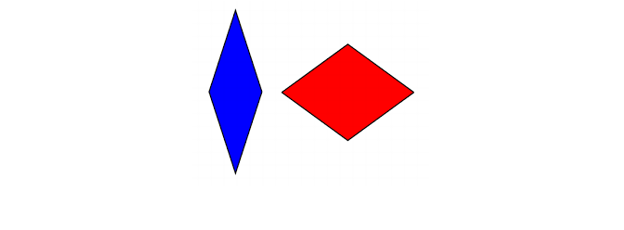
Penrose fliser (rombuser)
Du kan produsere mosaikk som sådan:
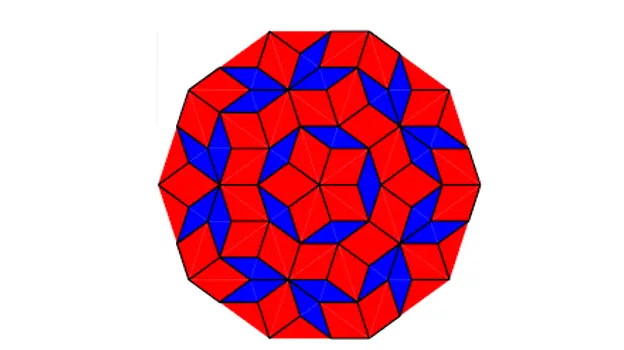
Penrose flislegging
Den andre av disse aperiodiske flisleggingene er gitt av to deler kjent som drage og pil, av åpenbare grunner:
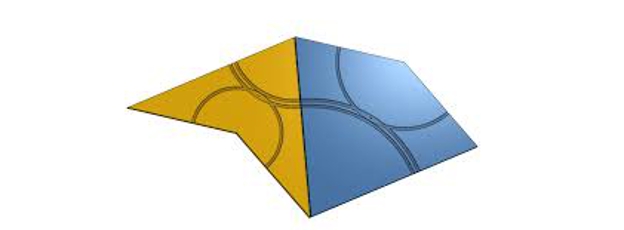
Penrose-fliser (komet og pil)
Vel, det er tvil om at en plantar kan være følgende:
Er det aperiodiske mosaikker dannet av en enkelt flis?
Dette problemet har vært kjent som Ein Stein-problemet (fra tysk for "en stein") og i nesten 50 år har det vært uløst. Inntil mars i fjor!
Oppdagelsen av Ein Stein
Den 20. mars publiserte forskerne David Smith, Joseph Samuel Myers, Craig S. Kaplan og Chaim Goodman-Strauss fra universitetene i Cambridge, Waterloo og Arkansas verket 'An aperiodic monotile' der de beskrev en mulig form for en svært ettertraktet etter tesserae som gir opphav til en aperiodisk mosaikk med et unikt stykke.
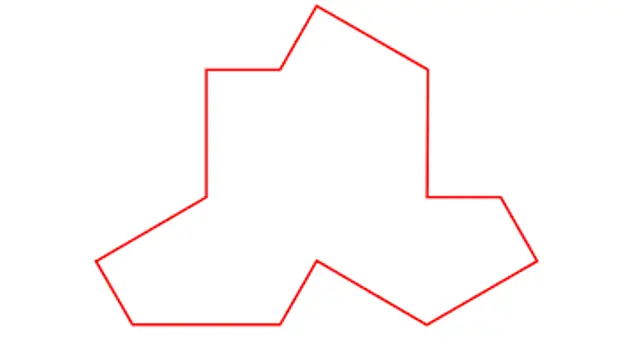
Tile beskrevet av Smith, Myers, Kaplan og Goodman-Strauss
Med denne enkeltflisen, som for meg virker å være veldig lik en T-skjorte, viser han at aperiodiske mosaikker som følgende kan bygges:

Aperiodisk mosaikk av en flis
Hvis nysgjerrigheten din er nøktern på emnet, kan du gå dypere inn i denne oppdagelsen i følgende video,
der oppdagerne snakker med andre relevante personer i området, inkludert Nobelprisen i fysikk Roger Penrose.
ABCdario de las Matemáticas er en seksjon som oppstår fra samarbeidet med formidlingskommisjonen til Royal Spanish Mathematical Society (RSME).
OM FORFATTEREN
Victor M. Manero

