– Stop met zoeken! We hebben het eindelijk gevonden', riep commissaris MacCarnigan uit.
– Wie meneer? vroeg tweede luitenant Pierron.
'Op een van de meest gladde schurken die je je maar kunt voorstellen. Ik ben er al bijna 50 jaar naar op zoek.
– Ik had geen idee, commissaris. Over wie gaat het?
– Zijn nummer is Ein Stein en het heeft me bijna een heel leven gekost om het te vinden.
- Over wie gaat het? Heb je daar foto's van jou?
– Ja, ik heb het hier, zo ziet het eruit, maar laat je niet misleiden door zijn onschuldige uiterlijk, deze meneer hier heeft ons bijna tien decennia in spanning gehouden.
Dus MacCarnigan liet Agent Pierron de foto van Ein Stein zien, deze foto:
In Stein.
Deze korte geschiedenis van politieagenten lijkt misschien een grap, maar als we detectives inruilen voor wiskundigen, wordt het een van de meest fantastische wiskundige ontdekkingen die de afgelopen jaren hebben plaatsgevonden. Maar om de reikwijdte van dit verhaal te begrijpen, moeten we het eerst hebben over een van de gebieden waarin wiskunde en kunst samensmelten: mozaïeken.
mozaïek kranten
We hebben allemaal wel eens een mozaïek gezien in ons leven. Dit zijn kleine artistieke of decoratieve werken die zijn gemaakt met behulp van kleine stukjes die in elkaar passen.


Enkele voorbeelden van mozaïeken
Als we het in de wiskunde hebben over mozaïeken, verwijzen we meestal naar wat bekend staat als vlakvullingen, wat een manier is om stukken of tegels zo te rangschikken dat deze stukken gemeenschappelijke randen hebben en geen gaten achterlaten.
Lang geleden stelden wiskundigen en wiskunde de volgende vraag
Met wat voor stukken kan ik het vliegtuig betegelen?
Dat wil zeggen, wat voor soort stukken kan ik daarvoor gebruiken, door ze zo te plaatsen dat de tegels elkaar aan gemeenschappelijke zijden raken, er zijn geen openingen in het vlak. Het is duidelijk dat de cirkels niet in deze selecte groep zitten, want als ik het vlak wil betegelen met alleen cirkels, blijven er gaten over. Kom op, ik moet vaste mortel gieten.

cirkels laten gaten achter
Er zijn echter nog veel meer vormen waarmee we het vlak kunnen betegelen, zoals driehoeken, vierkanten of zeshoeken.

Mozaïekpatroon met een enkele regelmatige veelhoek
Of we kunnen het vlak betegelen met combinaties van deze of andere figuren.

Mozaïekpatroon met verschillende regelmatige veelhoeken
Of je kunt het vliegtuig zelfs betegelen met meer extravagante combinaties:
Andere mogelijke betegelingen
Maar je hebt nagedacht over de grote verscheidenheid aan tegels die je hebt gepresenteerd, ze hebben allemaal iets gemeen, en dat is dat ze periodiek zijn. De term periodiek verwijst naar het feit dat er een andere vertaling is dan nul, waardoor het hele mozaïek hetzelfde blijft. Van wat we begrijpen, is het gelijk aan het feit dat als we een oppervlak betegelen, de ogen keramisch maken en iemand het hele mozaïek in een specifieke richting beweegt en vervolgens de ogen weer bedekt, we het verschil tussen het originele mozaïek niet kunnen waarderen en de ontheemde.
mozaïeken zonder kranten
In tegenstelling tot periodieke betegelingen vinden we niet-periodieke betegelingen, dat zijn die waarvoor er geen vertaling is, niet nul, waardoor het mozaïek er hetzelfde uitziet. Het is niet moeilijk om niet-periodieke mozaïeken te vinden, het is voldoende om bijvoorbeeld een periodieke tegel te nemen, laten we bijvoorbeeld denken aan een tegel die alleen uit vierkanten bestaat, en een enkel vierkant van het hele mozaïek is verdeeld in twee driehoeken . Het is duidelijk nog steeds een vlakvulling van het vlak, maar er zal geen enkele vertaling zijn die de hele tesserae hetzelfde zal laten, aangezien we in staat zullen zijn om onderscheid te maken tussen het originele mozaïek en het verplaatste mozaïek door simpelweg de gewijzigde positie van het vlak te observeren. twee driehoeken.
aperiodische tegels
Maar nu wordt het interessant, want dan verschijnt het concept van aperiodiek mozaïek, dat zijn mozaïeken die, hoewel ze niet periodiek zijn, voldoen aan de extra voorwaarde dat ze geen willekeurig grote periodieke regio's hebben. Op dezelfde manier kan dit idee worden gehoord als in een aperiodiek mozaïek: als we een stuk nemen dat groot genoeg is, wordt het niet herhaald in de rest van het mozaïek. Zorg ervoor dat het mozaïekmonster dat geen tijdschrift eerder beschrijft, niet aperiodiek is, aangezien we willekeurig grote regio's kunnen vinden die periodiek zijn, neem gewoon willekeurig grote stukken die geen van beide driehoeken bevatten.
Dus de vraag die zich natuurlijk voordoet is de volgende:
Zijn er aperiodische mozaïeken?
Deze vraag, die in de tweede helft van de vorige eeuw begon te worden bestudeerd, kreeg al snel een bevestigend antwoord en een van de eersten die een aperiodieke mozaïekpatroon vond, was Raphael M. Robinson. Het mozaïek beschreven door Robinson in 1971 bestond uit 6 opeenvolgende tesserae.

robinson-tegels
Een paar jaar later, eveneens in de jaren zeventig, verkreeg Roger Penrose twee aperiodische tegels die konden worden gebouwd, elk met slechts twee verschillende tegels. De eerste van deze vlakvullingen wordt gevormd door twee verschillende ruiten:
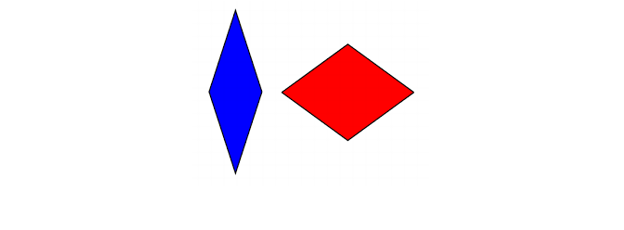
Penrose-tegels (ruiten)
U kunt mozaïeken als zodanig maken:
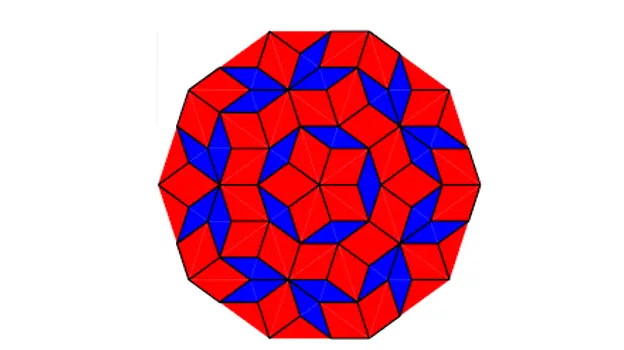
Penrose-tegels
De tweede van deze aperiodieke betegelingen wordt om voor de hand liggende redenen gegeven door twee stukken die bekend staan als vlieger en pijl:
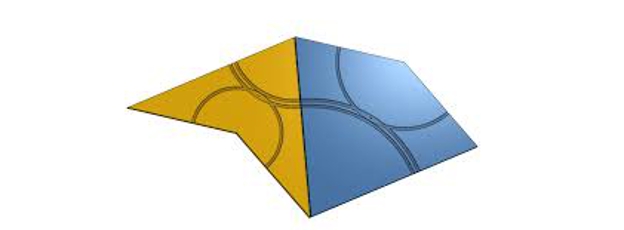
Penrose-tegels (komeet en pijl)
Welnu, er bestaat twijfel dat een voetzool het volgende zou kunnen zijn:
Zijn er aperiodische mozaïeken gevormd door een enkele tegel?
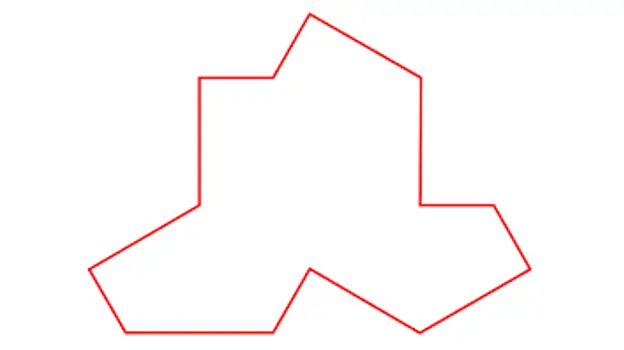
Dit probleem staat bekend als het Ein Stein-probleem (van het Duits voor "een steen") en is al bijna 50 jaar onopgelost gebleven. Tot afgelopen maart!
De ontdekking van de Ein Stein
Op 20 maart publiceerden wetenschappers David Smith, Joseph Samuel Myers, Craig S. Kaplan en Chaim Goodman-Strauss van de universiteiten van Cambridge, Waterloo en Arkansas het werk 'An aperiodic monotile' waarin ze een mogelijke vorm van de veelgevraagde na tesserae die aanleiding geeft tot een aperiodiek mozaïek met een uniek stuk.
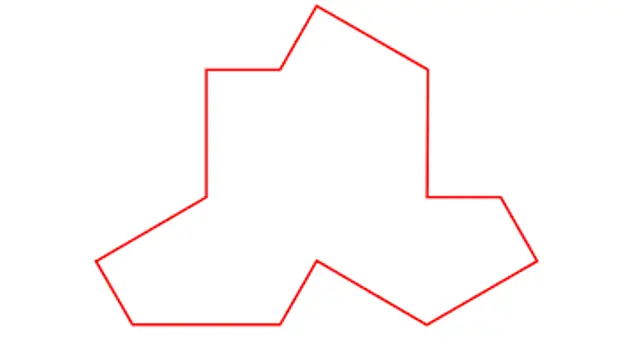
Tegel beschreven door Smith, Myers, Kaplan en Goodman-Strauss
Met deze enkele tegel, die volgens mij erg lijkt op een T-shirt, laat hij zien dat aperiodieke mozaïeken zoals de volgende kunnen worden gebouwd:

Aperiodiek mozaïek van een tegel
Als je nieuwsgierigheid naar het onderwerp nuchter is, kun je dieper op deze ontdekking ingaan in de volgende video,
waarin zijn ontdekkers spreken met andere relevante mensen in het gebied, waaronder de Nobelprijs voor natuurkunde Roger Penrose.
De ABCdario de las Matemáticas is een sectie die voortkomt uit de samenwerking met de Dissemination Commission van de Royal Spanish Mathematical Society (RSME).
OVER DE AUTEUR
Victor M. Manero

