- ຢຸດການຊອກຫາ! "ໃນທີ່ສຸດພວກເຮົາໄດ້ພົບເຫັນມັນ," ກໍາມະການ MacCarnigan ຮ້ອງອອກມາ.
– ໃຜແດ່? - ຖາມວ່າຮ້ອຍຕີ Pierron.
– ຕໍ່ຄົນຂີ້ຕົວະທີ່ຫຍາບຄາຍທີ່ສຸດທີ່ເຈົ້າສາມາດວາດພາບໄດ້. ຂ້ອຍຊອກຫາມັນມາເກືອບ 50 ປີແລ້ວ.
– ຂ້າພະເຈົ້າບໍ່ມີຄວາມຄິດເຫັນ, Commissioner. ມັນກ່ຽວກັບໃຜ?
– ຕົວເລກຂອງລາວແມ່ນ Ein Stein ແລະມັນໄດ້ເອົາຂ້ອຍເກືອບຕະຫຼອດຊີວິດເພື່ອຊອກຫາລາວ.
- ມັນກ່ຽວກັບໃຜ? ເຈົ້າມີຮູບຂອງເຈົ້າຢູ່ທີ່ນັ້ນບໍ?
- ແມ່ນແລ້ວ, ຂ້ອຍມີມັນຢູ່ທີ່ນີ້, ນີ້ແມ່ນສິ່ງທີ່ມັນຄ້າຍຄື, ແຕ່ຢ່າຫລອກລວງດ້ວຍຮູບລັກສະນະທີ່ບໍລິສຸດຂອງມັນ, ຜູ້ຊາຍນ້ອຍໆຢູ່ທີ່ນີ້ໄດ້ຮັກສາພວກເຮົາຢູ່ໃນຄວາມແປກໃຈເກືອບສິບທົດສະວັດ.
MacCarnigan ຫຼັງຈາກນັ້ນໄດ້ສະແດງ Agent Pierron ຮູບຂອງ Ein Stein, ຮູບນີ້:
ໃນ Stein.
ເລື່ອງຕໍາຫຼວດສັ້ນໆນີ້ອາດຈະເບິ່ງຄືວ່າເປັນເລື່ອງຕະຫລົກ, ແຕ່ຖ້າພວກເຮົາປ່ຽນນັກສືບສໍາລັບນັກຄະນິດສາດ, ມັນຈະກາຍເປັນຫນຶ່ງໃນການຄົ້ນພົບທາງຄະນິດສາດທີ່ປະເສີດທີ່ສຸດທີ່ມີປະສົບການໃນຊຸມປີທີ່ຜ່ານມາ. ແຕ່ເພື່ອເຂົ້າໃຈຂອບເຂດຂອງເລື່ອງນີ້, ກ່ອນອື່ນ ໝົດ, ພວກເຮົາຕ້ອງເວົ້າກ່ຽວກັບ ໜຶ່ງ ໃນສາຂາທີ່ຄະນິດສາດແລະສິລະປະປະສົມປະສານ: mosaics.
ໜັງສືພິມ Mosaic
ພວກເຮົາທຸກຄົນໄດ້ເຫັນ mosaic ໃນບາງຈຸດໃນຊີວິດຂອງພວກເຮົາ. ນີ້ແມ່ນວຽກງານສິລະປະຂະຫນາດນ້ອຍຫຼືການຕົກແຕ່ງທີ່ເຮັດດ້ວຍການນໍາໃຊ້ຕ່ອນຂະຫນາດນ້ອຍທີ່ເຫມາະຮ່ວມກັນ.


ບາງຕົວຢ່າງຂອງ mosaics
ໃນເວລາທີ່ພວກເຮົາສົນທະນາກ່ຽວກັບ mosaics ໃນຄະນິດສາດ, ພວກເຮົາປົກກະຕິຫມາຍເຖິງສິ່ງທີ່ເອີ້ນວ່າ tessellations, ເຊິ່ງເປັນວິທີການຈັດຕ່ອນຫຼືກະເບື້ອງເພື່ອໃຫ້ຕ່ອນເຫຼົ່ານີ້ມີແຄມທົ່ວໄປແລະບໍ່ອອກຈາກຮູ.
ເມື່ອດົນນານມາແລ້ວ, ນັກຄະນິດສາດໄດ້ຖາມຕົວເອງວ່າ:
ປະເພດໃດແດ່ທີ່ຂ້ອຍສາມາດ tessellate ຍົນດ້ວຍ?
ນັ້ນແມ່ນ, ປະເພດໃດແດ່ທີ່ຂ້ອຍສາມາດໃຊ້ສໍາລັບການນັ້ນ, ວາງພວກມັນເພື່ອໃຫ້ກະເບື້ອງແຕະໃສ່ດ້ານທົ່ວໄປ, ບໍ່ມີຊ່ອງຫວ່າງໃນຍົນ. ເຫັນໄດ້ຊັດເຈນວ່າວົງມົນບໍ່ໄດ້ຢູ່ໃນກຸ່ມທີ່ເລືອກນີ້, ເພາະວ່າຖ້າຂ້ອຍຕ້ອງການວາງແຜ່ນຍົນໂດຍໃຊ້ພຽງແຕ່ວົງມົນເທົ່ານັ້ນ, ມັນຈະມີຊ່ອງຫວ່າງ. ມາ, ຂ້ອຍຈະຕ້ອງໃສ່ grout ຄົງທີ່.

ວົງການປ່ອຍໃຫ້ຊ່ອງຫວ່າງ
ຢ່າງໃດກໍຕາມ, ມີຕົວເລກອື່ນໆຈໍານວນຫຼາຍທີ່ພວກເຮົາສາມາດ tessellate ຍົນ, ເຊັ່ນ, ສໍາລັບການຍົກຕົວຢ່າງ, ສາມຫຼ່ຽມ, ສີ່ຫລ່ຽມຫຼື hexagons.

Tessellation ກັບ polygon ປົກກະຕິດຽວ
ຫຼືພວກເຮົາສາມາດກະເບື້ອງຍົນດ້ວຍການປະສົມຂອງຕົວເລກເຫຼົ່ານີ້ຫຼືອື່ນໆ.

Tessellation ກັບ polygons ປົກກະຕິຫຼາຍ
ຫຼືແມ້ກະທັ້ງສາມາດ tessellate ຍົນດ້ວຍການປະສົມ extravagant ຫຼາຍ:
tessellations ທີ່ເປັນໄປໄດ້ອື່ນໆ
ແຕ່ລາວໄດ້ພິຈາລະນາຄວາມຫລາກຫລາຍຂອງ tessellations ທີ່ລາວໄດ້ນໍາສະເຫນີ, ພວກມັນທັງຫມົດມີບາງສິ່ງບາງຢ່າງທີ່ຄ້າຍຄືກັນ, ແລະນັ້ນແມ່ນ, ແຕ່ລະໄລຍະ. ຄໍາວ່າໄລຍະເວລາຫມາຍເຖິງຄວາມຈິງທີ່ວ່າມີການແປບາງຢ່າງ, ນອກເຫນືອໄປຈາກສູນ, ທີ່ເຮັດໃຫ້ mosaic ທັງຫມົດຄືກັນ. ຈາກສິ່ງທີ່ພວກເຮົາເຂົ້າໃຈ, ມັນເທົ່າກັບວ່າຖ້າພວກເຮົາກະເບື້ອງພື້ນຜິວ, ເຊລາມິກຕາແລະຜູ້ໃດຜູ້ຫນຶ່ງຍ້າຍ mosaic ທັງຫມົດໄປໃນທິດທາງສະເພາະໃດຫນຶ່ງແລະຫຼັງຈາກນັ້ນກວມເອົາຕາອີກເທື່ອຫນຶ່ງພວກເຮົາຈະບໍ່ສາມາດເຂົ້າໃຈຄວາມແຕກຕ່າງລະຫວ່າງ mosaic ຕົ້ນສະບັບແລະການຍົກຍ້າຍ. ຫນຶ່ງ.
Mosaics ໂດຍບໍ່ມີຫນັງສືພິມ
ໃນທາງກົງກັນຂ້າມກັບ tessellations ແຕ່ລະໄລຍະ, ພວກເຮົາພົບເຫັນ tessellations ທີ່ບໍ່ແມ່ນໄລຍະເວລາ, ເຊິ່ງແມ່ນບໍ່ມີການແປ, ບໍ່ແມ່ນ null, ເຊິ່ງເຮັດໃຫ້ mosaic ມີລັກສະນະດຽວກັນ. ມັນບໍ່ແມ່ນເລື່ອງຍາກທີ່ຈະຊອກຫາ mosaic ທີ່ບໍ່ມີໄລຍະເວລາ, ມັນພຽງພໍ, ສໍາລັບການຍົກຕົວຢ່າງ, ໃຊ້ເວລາ tessellation ເປັນໄລຍະ, ໃຫ້ພວກເຮົາຄິດຕົວຢ່າງຫນຶ່ງທີ່ສ້າງຂຶ້ນພຽງແຕ່ສີ່ຫລ່ຽມ, ແລະພວກເຮົາແບ່ງເປັນສີ່ຫຼ່ຽມມົນດຽວຂອງ mosaic ທັງຫມົດເປັນສອງສາມຫຼ່ຽມ. ເຫັນໄດ້ຊັດເຈນວ່າມັນເປັນການແຜ່ກະຈາຍຂອງຍົນ, ແຕ່ຈະບໍ່ມີການແປທີ່ປ່ອຍໃຫ້ tessera ທັງຫມົດຄືກັນເພາະວ່າພວກເຮົາຈະສາມາດຈໍາແນກລະຫວ່າງ mosaic ຕົ້ນສະບັບແລະຫນຶ່ງທີ່ຖືກຍົກຍ້າຍຂອງມັນພຽງແຕ່ໂດຍການສັງເກດເບິ່ງຕໍາແຫນ່ງດັດແກ້ຂອງສາມຫຼ່ຽມສອງ.
mosaics aperiodic
ແຕ່ໃນປັດຈຸບັນແມ່ນເວລາທີ່ສິ່ງຕ່າງໆໄດ້ຮັບຄວາມສົນໃຈ, ເພາະວ່າມັນແມ່ນເວລາທີ່ແນວຄວາມຄິດຂອງ mosaic aperiodic ປາກົດ, ເຊິ່ງເປັນໄລຍະເວລາ, ບໍ່ພໍໃຈກັບເງື່ອນໄຂເພີ່ມເຕີມທີ່ພວກເຂົາບໍ່ມີພື້ນທີ່ຂະຫນາດໃຫຍ່ຕາມລໍາດັບ. ໃນທາງດຽວກັນຄວາມຄິດນີ້ສາມາດໄດ້ຍິນຄືກັບ mosaic aperiodic, ຖ້າພວກເຮົາເອົາຊິ້ນສ່ວນຂະຫນາດໃຫຍ່ພຽງພໍ, ມັນຈະບໍ່ຊ້ໍາອີກໃນສ່ວນທີ່ເຫລືອຂອງ mosaic. ໃຫ້ແນ່ໃຈວ່າຕົວຢ່າງ mosaic ທີ່ບໍ່ມີການອະທິບາຍໄລຍະເວລາກ່ອນບໍ່ແມ່ນ aperiodic ເນື່ອງຈາກພວກເຮົາສາມາດຊອກຫາພື້ນທີ່ຂະຫນາດໃຫຍ່ຕາມລໍາດັບ, ພຽງແຕ່ເອົາຕ່ອນໃຫຍ່ທີ່ກໍານົດເອງທີ່ບໍ່ປະກອບມີສາມຫຼ່ຽມ.
ດັ່ງນັ້ນຄໍາຖາມທີ່ເກີດຂຶ້ນຕາມທໍາມະຊາດແມ່ນນີ້:
ມີ mosaics aperiodic ບໍ?
ຄໍາຖາມນີ້, ເຊິ່ງໄດ້ເລີ່ມຕົ້ນທີ່ຈະສົນທະນາໃນເຄິ່ງທີ່ສອງຂອງສະຕະວັດທີ່ຜ່ານມາ, ທັນທີທັນໃດໄດ້ຮັບຄໍາຕອບທີ່ຢືນຢັນແລະຫນຶ່ງໃນທໍາອິດທີ່ຊອກຫາ tessellation aperiodic ແມ່ນ Raphael M. Robinson. mosaic ອະທິບາຍໂດຍ Robinson ໃນ 1971 ແມ່ນປະກອບດ້ວຍ 6 ກະເບື້ອງຕິດຕໍ່ກັນ.

ກະເບື້ອງ Robinson
ສອງສາມປີຕໍ່ມາ, ໃນຊຸມປີ 70, Roger Penrose ໄດ້ຮັບກະເບື້ອງ aperiodic ສອງແຜ່ນທີ່ສາມາດກໍ່ສ້າງໄດ້, ແຕ່ລະແຜ່ນໃຊ້ພຽງແຕ່ສອງກະເບື້ອງທີ່ແຕກຕ່າງກັນ. ທໍາອິດຂອງ tessellations ເຫຼົ່ານີ້ແມ່ນປະກອບດ້ວຍສອງ rhombuses ທີ່ແຕກຕ່າງກັນ:
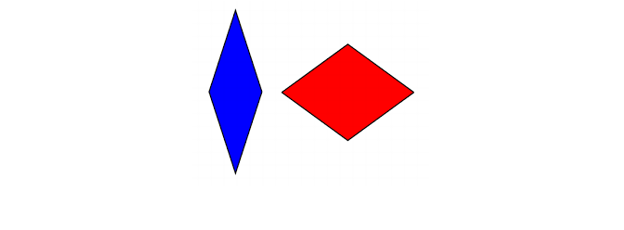
Penrose tesserae (rhombuses)
ທ່ານສາມາດຜະລິດ mosaic ດັ່ງກ່າວ:
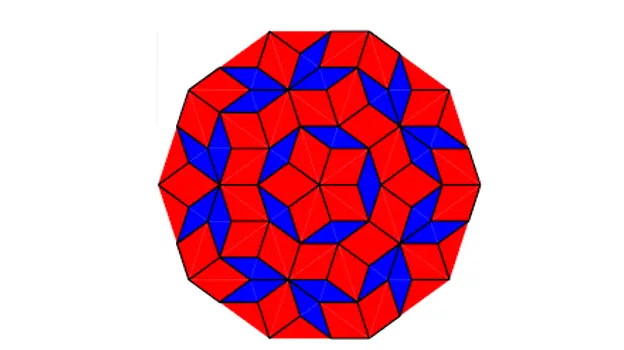
Penrose Mosaic
ອັນທີສອງຂອງ tessellations aperiodic ເຫຼົ່ານີ້ແມ່ນໃຫ້ໂດຍສອງຊິ້ນທີ່ເອີ້ນວ່າ comet ແລະລູກສອນ, ສໍາລັບເຫດຜົນທີ່ຊັດເຈນ:
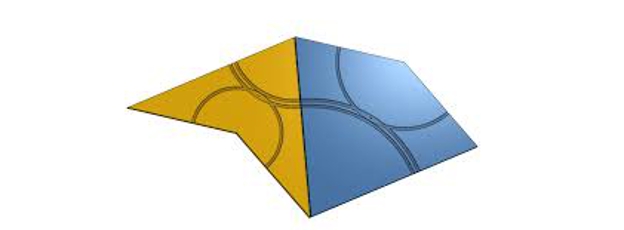
Penrose tesserae (ວ່າວ ແລະລູກສອນ)
ແລ້ວ, ມີຄໍາຖາມທີ່ວ່າ plantar ສາມາດເປັນດັ່ງຕໍ່ໄປນີ້:
ມີ mosaics aperiodic ປະກອບດ້ວຍກະເບື້ອງດຽວບໍ?
ບັນຫານີ້ໄດ້ຖືກເອີ້ນວ່າບັນຫາ Ein Stein (ຈາກພາສາເຢຍລະມັນສໍາລັບ "ກ້ອນຫີນ") ແລະເກືອບ 50 ປີມັນຍັງຄົງບໍ່ໄດ້ຮັບການແກ້ໄຂ. ຈົນຮອດເດືອນມີນາທີ່ຜ່ານມາ!
ການຄົ້ນພົບຂອງ Ein Stein
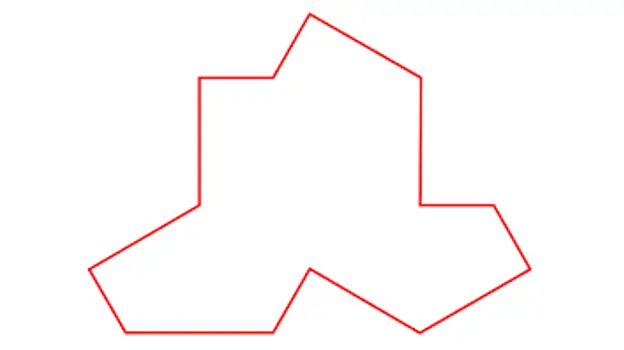
ໃນວັນທີ 20 ເດືອນມີນາ, ນັກວິທະຍາສາດ David Smith, Joseph Samuel Myers, Craig S. Kaplan ແລະ Chaim Goodman-Strauss ຈາກມະຫາວິທະຍາໄລ Cambridge, Waterloo ແລະ Arkansas ໄດ້ພິມເຜີຍແຜ່ວຽກງານ 'An aperiodic monotile' ເຊິ່ງພວກເຂົາໄດ້ອະທິບາຍເຖິງຮູບແບບທີ່ເປັນໄປໄດ້ຂອງການສະແຫວງຫາດັ່ງກ່າວ. - ຫຼັງຈາກກະເບື້ອງທີ່ເຮັດໃຫ້ເກີດເປັນ mosaic aperiodic ມີສິ້ນເປັນເອກະລັກ.
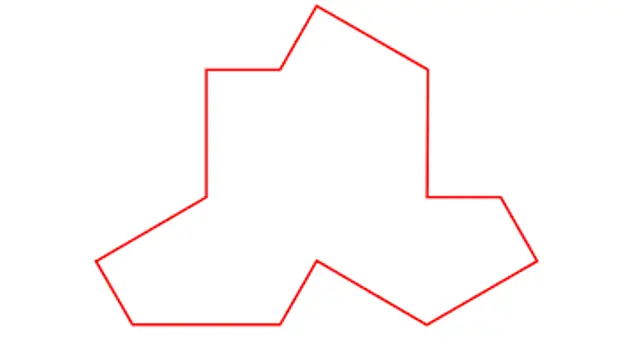
ກະເບື້ອງອະທິບາຍໂດຍ Smith, Myers, Kaplan ແລະ Goodman-Strauss
ດ້ວຍກະເບື້ອງດຽວນີ້, ເຊິ່ງໃນຄວາມຄິດເຫັນຂອງຂ້ອຍເບິ່ງຄືວ່າຄ້າຍຄືກັນກັບເສື້ອທີເຊີດ, ມັນສະແດງໃຫ້ເຫັນວ່າ mosaics aperiodic ຄືກັບສິ່ງຕໍ່ໄປນີ້ສາມາດສ້າງໄດ້:

mosaic aperiodic ຂອງກະເບື້ອງ
ຖ້າຫາກວ່າທ່ານຢາກຮູ້ສຶກຢາກເຫັນກ່ຽວກັບຫົວຂໍ້, ທ່ານສາມາດ delve ເລິກເຂົ້າໄປໃນການຄົ້ນພົບນີ້ໃນວິດີໂອຕໍ່ໄປນີ້,
ເຊິ່ງຜູ້ຄົ້ນພົບຂອງມັນເວົ້າກັບຜູ້ທີ່ກ່ຽວຂ້ອງອື່ນໆໃນພື້ນທີ່, ລວມທັງລາງວັນໂນແບລດ້ານຟີຊິກສາດ Roger Penrose.
ຄະນິດສາດ ABCdario de las ແມ່ນພາກທີ່ເກີດຂື້ນຈາກການຮ່ວມມືກັບຄະນະກໍາມະການເຜີຍແຜ່ຂອງ Royal Spanish Mathematical Society (RSME).
ກ່ຽວກັບຜູ້ຂຽນ
Victor M. Manero

