– Desine investigationem! Invenimus tandem,' inquit Commissarius MacCarnigan.
– Quis domine? rogavit alterum locumtenentem Pierron.
“Ad unum e lubricissimis improbos umquam excogitare potuisti. Five 50 annos quaesivi.
— Nesciebam, Commissarius. Quis est de eo?
– Numerus eius est Ein Stein et me paene vitam invenire.
- Quis id est? Habesne imagines te ibi?
– Imo mihi hic placet, hoc est quod videtur, sed ne specie innocens delusus, hic nos decem fere decenniis suspensos servavit hic vir.
Ita MacCarnigan ostendit Agentem Pierronem photographicam Ein Stein, hanc imaginem photographicam;
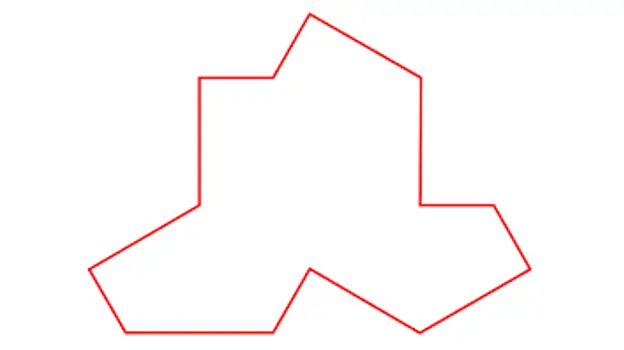
Apud Stein.
Haec brevis historia vigilum quasi iocus videri potest, sed si detectivas mathematicis mutamus, fit una ex mirabilibus inventis mathematicis quae his annis facta sunt. Sed ut huius fabulae scopum intelligamus, primum loqui debemus de uno campo in quo mathematica et ars miscentur: crustis.
ephemerides tessellis
Omnes musivum vidimus in aliquo loco in vita nostra. Haec parva sunt opera artificiosa vel decorativa quae utentes frusta quae in unum cohaerent fiunt.


Exempla quaedam lapillis
Cum de crustis in mathematicis loquimur, plerumque tessellationes notae sunt referre, quod est modus disponendi frusta vel tegularum ut partes communes habeant oras et foramina non relinquent.
Jamdiu mathematici et mathematici sequentem quaestionem moverunt
Quales partes possum tegulare planum?
Hoc est, quo genere frusta utar ad id, ut tegulae communibus lateribus se tangant ponens, non sunt hiatus in consilio. Plane circuli non sunt in hoc coetu selecto, quia si voles planum tegere utentibus solis circulis, me pertusum relinquent. Age, certum grout conjicere vado.

circulos relinquere hiatus
Sunt autem multae aliae figurae, quibus tegulare planum possumus, ut triangula, quadrata vel hexagona.

Tessellatum polygonum cum uno regulari
Vel possumus tegere planum cum combinationibus harum vel aliarum figurarum.

Tessellatum polygonorum aliquot regularium
Vel potes vel tegula plana cum junctis largioribus;
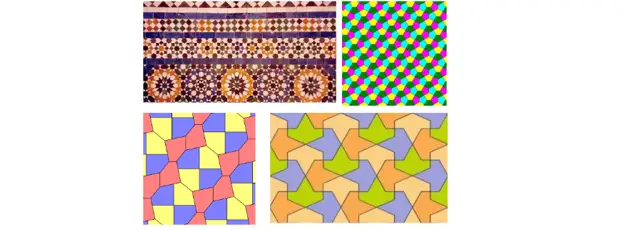
Aliae res possibilia sunt
Sed magnam paiium quam exhibuistis varietatem considerasti, omnibus aliquid commune habentibus, id est, ut periodica sint. Vocabulum periodicum ad hoc significat, translationem aliquam esse, praeter nulla, quae totum idem musivum relinquit. Ex iis quae intelligimus, aequiparabile est quod si superficies, ceramicam oculos texamus, et quis totam musivam in determinato directione moveat et oculos iterum tegat, non poterimus cognoscere differentiam inter mosaicam originalem. et luxatis unum.
lapillis sine ephemerides
E contra periodicas paiitiones non-periodicas reperimus, quae sunt illae quarum nulla est translatio, non nulla, quae musivo eadem specie relinquit. Non difficile est invenire musivos non periodicos, satis est, exempli gratia, tegulam periodicam sumere, putemus, exempli gratia, unum tantum quadratis formatum, et unum quadratum totius musivi in duo triangula divisum. . Plane adhuc est planum tessellatum, sed nulla translatio erit quae totam tesserulam eandem relinquet, quandoquidem inter mosaicum originalem et eius loco mutatum simpliciter distinguere poterimus. duo triangula.
periodica tegula
Nunc autem cum res iucunda sunt, quia cum notio musivo aperiodica apparet, quae sunt illae, licet periodica non sint, condicionem extra satisfaciunt quod regiones periodicas non habent arbitrio magnas. Eodem modo audiri potest haec idea ut in musivo aperiodico, si satis amplum sumatur, non repetitur in reliquo musivo. Fac ut exemplum musivum quod nullum periodicum prius describit, non est periodicum, quandoquidem possumus invenire regiones magnas quae periodicas arbitratu sunt, modo capias ad libitum magnas partes quae vel triangulum non comprehendunt.
Quaeritur ergo naturaliter talis:
Suntne crustis periodicis?
Quaestio haec, quae secundo dimidio saeculo superiore indagari coepit, mox responsum affirmativum accepit et una ex primis ad inveniendam tessellationem aperiodicam Raphael M. Robinson fuit. Mosaicum a Robinson anno 1971 descriptum 6 continuos tesserae constabat.

Robinson tegulas
Paucis annis post, etiam annis 70, Roger Penrose duas tegulas aperiodicas aedificandas consecutus est, singulis tantum duobus diversis tegulis utens. Primum ex his tessellatum duobus rhombus diversum formatur;
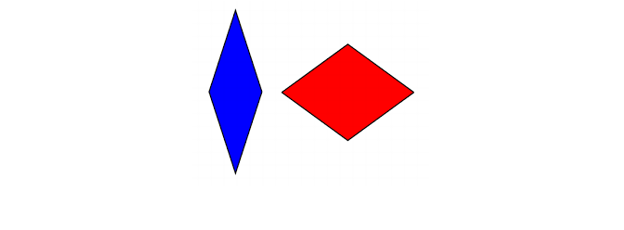
Tegulae penrosae (rhombuses)
Mosaica producere potes ut talia:
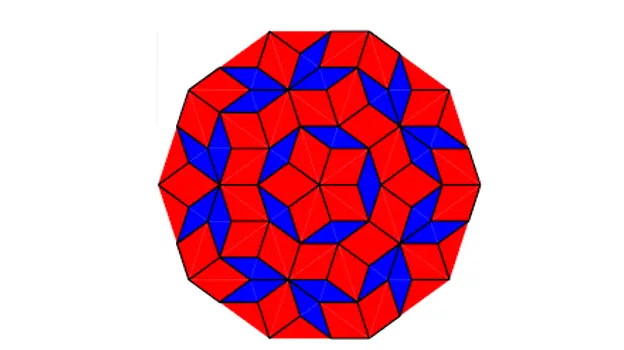
Penrose tegula
Secunda harum paiitionum aperiodicarum a duobus fragmentis quae milvi et sagittae dicuntur, evidentibus de causis;
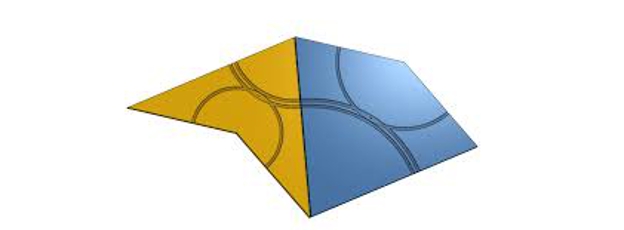
Tegulae penrosae (comet et sagitta)
Bene dubium est quin plantare possit esse talis;
Suntne musivi aperiodici per unam tegulam formati?
Hoc problema notum est sicut problema Ein Stein (e Germanico pro "lapide") et per 50 fere annos insolutam mansit. Usque ad ultimum Martii!
Inventio Ein Stein
Die XX Martii docti David Smith, Joseph Samuel Myers, Craig S. Kaplan et Chaim Goodman-Strauss ex Universitatibus Cantabrigiensis, Waterloo et Arkansas opus ediderunt 'Monotile aperiodicae monotile' in quo descripsere formam possibilem exquisitae quaesitae. post tessulam oritur musivo aperiodico cum particula singulari.
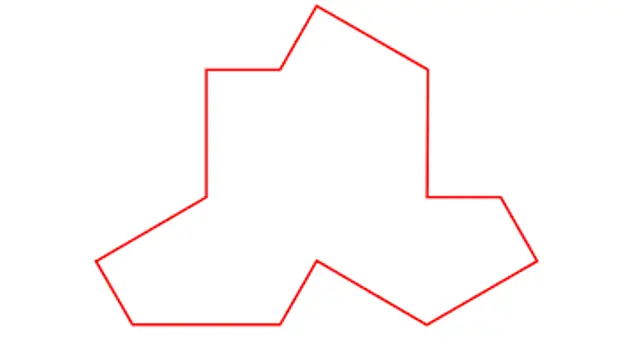
Tegula descripta a Smith, Myers, Kaplan et Goodman-Strauss
Cum hac una tegula, quae mihi simillima esse videtur subucula, ostendit musivos aperiodicos similes construi posse;

Mosaic tegularum
Si curiositas tua est de re sobria, altius in hanc inventionem in hoc video intendere potes.
in quibus eius inventores cum aliis pertinentibus hominibus in provincia loquuntur, inter Praemium Nobelianum Physicorum Roger Penrose.
De ABCdario de las Matemáticas sectio oritur ex collaboratione cum Commissione Disseminationis Societatis Mathematicae Regiae Hispanicae (RSME).
DE AUCTORE
Victor M. Manero

