-¡Para a busca! "Finalmente atopámolo", exclamou o comisario MacCarnigan.
—¿A quen señor? -preguntou o tenente segundo Pierron.
– A un dos canallas máis esquivos que nunca puideses imaxinar. Levo case 50 anos buscándoo.
– Non tiña nin idea, comisario. De quen se trata?
– O seu número é Ein Stein e levoume case toda unha vida atopalo.
- De quen se trata? Tes algunha foto túa alí?
– Si, téñoo aquí mesmo, así parece, pero non vos deixedes enganar polo seu aspecto inocente, este señorito de aquí tennos en suspenso dende hai case dez décadas.
MacCarnigan mostrou entón ao axente Pierron a foto de Ein Stein, esta foto:
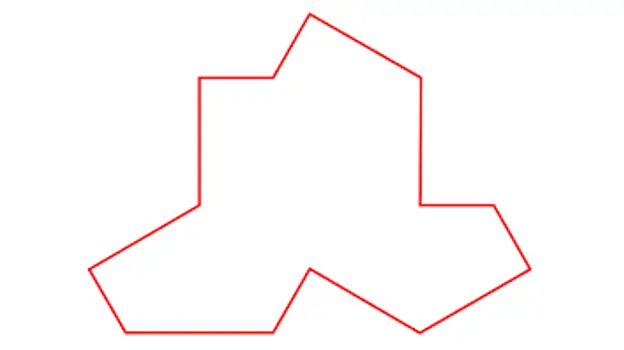
En Stein.
Esta breve historia policial pode parecer unha broma, pero se cambiamos de detectives por matemáticos, convértese nun dos descubrimentos matemáticos máis marabillosos que se viviron nos últimos anos. Pero para comprender o alcance desta historia hai que falar primeiro dun dos campos nos que se funden as matemáticas e a arte: os mosaicos.
Xornais Mosaicos
Todos vimos un mosaico nalgún momento das nosas vidas. Trátase de pequenas obras artísticas ou decorativas que se realizan mediante pequenas pezas que encaixan entre si.


Algúns exemplos de mosaicos
Cando falamos de mosaicos en matemáticas adoitamos referirnos ao que se coñece como teselado, que é unha forma de dispor pezas ou tellas para que estas pezas teñan bordos comúns e non deixen buratos.
Hai moito tempo, os matemáticos facíanse a seguinte pregunta:
Con que tipo de pezas podo teselar o avión?
É dicir, que tipo de pezas podo utilizar para iso, colocándoas para que as tellas toquen lados comúns, non haxa ocos no plano. Está claro que os círculos non están neste grupo selecto, xa que se quero en mosaico o plano usando só círculos quedarán ocos. Veña, que vou ter que poñer lechada fixa.

Os círculos deixan ocos
Porén, hai moitas outras figuras coas que podemos teselar o plano, como, por exemplo, triángulos, cadrados ou hexágonos.

Teselación cun único polígono regular
Ou podemos baldosar o plano con combinacións destas ou outras figuras.

Teselación con varios polígonos regulares
Ou incluso podes teselar o avión con combinacións máis extravagantes:
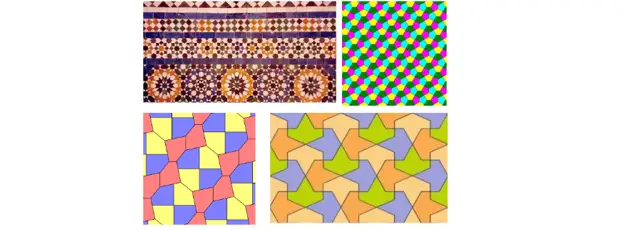
Outras posibles teselacións
Pero considerou a gran variedade de teselados que presentou, todos teñen algo en común, é dicir, son periódicos. O termo periódico refírese a que hai algunha tradución, distinta de cero, que deixa igual a todo o mosaico. Polo que entendemos, equivale a que se mosaicamos unha superficie, cerámica os ollos e alguén move todo o mosaico nunha dirección determinada e despois tapamos de novo os ollos non seremos capaces de apreciar a diferenza entre o mosaico orixinal e o desprazado. un.
Mosaicos sen xornais
En contraste coas teselas periódicas atopamos teselacións non periódicas, que son aquelas para as que non hai traslación, nin nula, que deixa o mosaico co mesmo aspecto. Non é difícil atopar mosaicos non periódicos, abonda, por exemplo, con tomar unha teselación periódica, pensemos por exemplo unha formada só por cadrados, e dividimos un só cadrado de todo o mosaico en dous triángulos. Está claro que non deixa de ser un teselado do plano, pero non haberá traslación que deixe igual a teselada enteira xa que poderemos distinguir entre o mosaico orixinal e o desprazado simplemente observando a posición modificada dos dous triángulos.
Mosaicos aperiódicos
Pero agora é cando a cousa se pon interesante, porque é cando aparece o concepto de mosaico aperiódico, que son aqueles que, sendo periódicos, non cumpren a condición extra de que non teñan rexións arbitrariamente grandes que sexan periódicas. Do mesmo xeito que se escoita esta idea como nun mosaico aperiódico, se tomamos unha peza suficientemente grande, non se repite no resto do mosaico. Asegúrate de que a mostra de mosaico que ningunha publicación periódica describe antes non é aperiódica xa que podemos atopar rexións arbitrariamente grandes que son periódicas, só tes que coller pezas arbitrariamente grandes que non inclúan ningún triángulo.
Entón, a pregunta que xorde naturalmente é a seguinte:
Existen mosaicos aperiódicos?
Esta pregunta, que comezou a ser discutida na segunda metade do século pasado, pronto recibiu unha resposta afirmativa e un dos primeiros en atopar unha teselación aperiódica foi Raphael M. Robinson. O mosaico descrito por Robinson en 1971 estaba formado por 6 fichas sucesivas.

Azulexos Robinson
Uns anos máis tarde, tamén na década de 70, Roger Penrose obtivo dúas tellas aperiódicas que se podían construír, utilizando cada unha só dúas tellas diferentes. A primeira destas teselacións está formada por dous rombos diferentes:
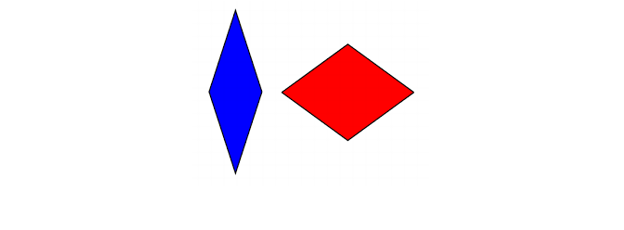
Teselas de Penrose (rombos)
Podes producir mosaicos como tal:
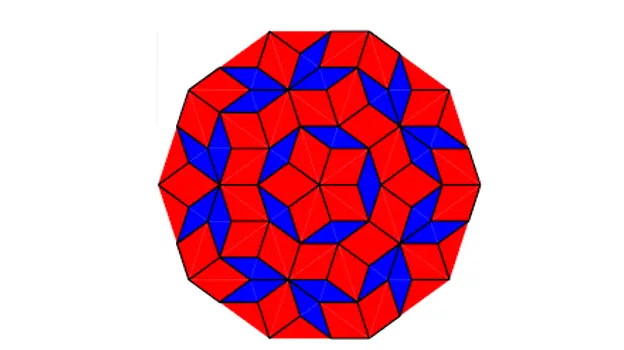
Mosaico de Penrose
A segunda destas teselacións aperiódicas vén dada por dúas pezas coñecidas como o cometa e a frecha, por razóns obvias:
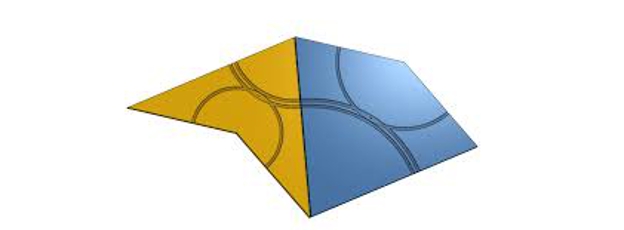
Teselas de Penrose (cometa e frecha)
Ben, hai a pregunta de que un plantar pode ser o seguinte:
Existen mosaicos aperiódicos formados por unha soa tella?
Este problema foi coñecido como o problema de Ein Stein (do alemán para "unha pedra") e durante case 50 anos permaneceu sen resolver. Ata o pasado mes de marzo!
O descubrimento de Ein Stein
O 20 de marzo, os científicos David Smith, Joseph Samuel Myers, Craig S. Kaplan e Chaim Goodman-Strauss das Universidades de Cambridge, Waterloo e Arkansas publicaron o traballo 'An aperiodic monotile' no que describían unha posible forma do tan buscado. -tras tella que dá lugar a un mosaico aperiódico cunha peza única.
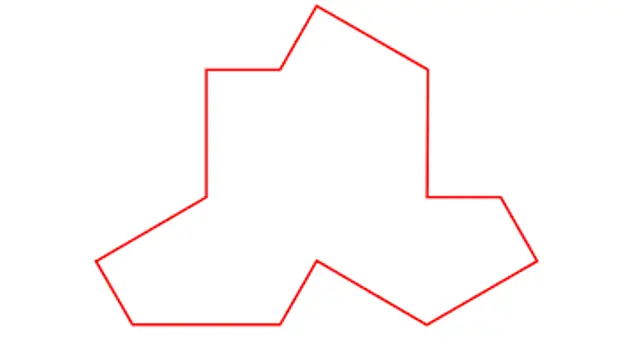
Tile descrito por Smith, Myers, Kaplan e Goodman-Strauss
Con este azulexo único, que na miña opinión se parece moito a unha camiseta, demostra que se poden construír mosaicos aperiódicos como os seguintes:

Mosaico aperiódico dunha tella
Se tes curiosidade polo tema, podes afondar neste descubrimento no seguinte vídeo,
na que os seus descubridores falan con outras persoas relevantes da zona, entre elas o Premio Nobel de Física Roger Penrose.
O ABCdario de las Matemáticas é unha sección que xorde da colaboración coa Comisión de Difusión da Real Sociedade Española de Matemáticas (RSME).
SOBRE O AUTOR
Víctor M. Manero

