– Arrêtez la recherche ! Nous l'avons enfin trouvé », s'est exclamé le commissaire MacCarnigan.
– Qui monsieur ? demanda le sous-lieutenant Pierron.
"À l'un des voleurs les plus glissants que vous puissiez imaginer. Je le cherche depuis près de 50 ans.
– Je n'en avais aucune idée, Monsieur le Commissaire. C'est à propos de qui?
– Son numéro est Ein Stein et il m'a fallu presque toute une vie pour le trouver.
- C'est à propos de qui? Avez-vous des photos de vous là-bas?
– Oui, je l'ai juste ici, c'est à ça qu'il ressemble, mais ne vous fiez pas à son apparence innocente, ce monsieur nous tient en haleine depuis près de dix décennies.
Alors MacCarnigan a montré à l'agent Pierron la photo d'Ein Stein, cette photo :
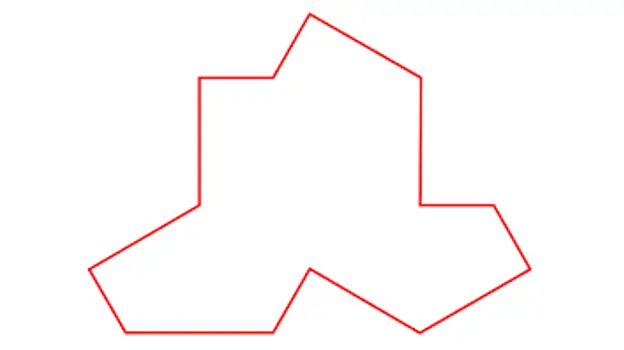
À Stein.
Cette brève histoire des policiers peut sembler une blague, mais si l'on change les détectives pour des mathématiciens, cela devient l'une des plus belles découvertes mathématiques de ces dernières années. Mais pour comprendre la portée de cette histoire, il faut d'abord parler d'un des domaines où les mathématiques et l'art se confondent : les mosaïques.
journaux en mosaïque
Nous avons tous vu une mosaïque à un moment donné de notre vie. Ce sont de petites œuvres artistiques ou décoratives qui sont réalisées à partir de petites pièces qui s'emboîtent.


Quelques exemples de mosaïques
Lorsque nous parlons de mosaïques en mathématiques, nous nous référons généralement à ce que l'on appelle des pavages, qui sont une manière d'arranger des pièces ou des tuiles de sorte que ces pièces aient des bords communs et ne laissent pas de trous.
Il y a longtemps, les mathématiciens et les mathématiques ont posé la question suivante
Avec quel type de pièces puis-je carreler l'avion ?
C'est-à-dire quel type de pièces puis-je utiliser pour cela, en les plaçant de manière à ce que les tuiles se touchent sur les côtés communs, il n'y a pas de lacunes dans le plan. Il est clair que les cercles ne font pas partie de ce groupe de sélection, car si je veux carreler le plan en utilisant uniquement des cercles, ils me laisseront des trous. Allez, je vais devoir couler du coulis fixe.

les cercles laissent des trous
Cependant, il existe de nombreuses autres formes avec lesquelles nous pouvons paver le plan, telles que des triangles, des carrés ou des hexagones.

Tessellation avec un seul polygone régulier
Ou nous pouvons carreler le plan avec des combinaisons de ces chiffres ou d'autres.

Tessellation avec plusieurs polygones réguliers
Ou vous pouvez même carreler l'avion avec des combinaisons plus extravagantes :
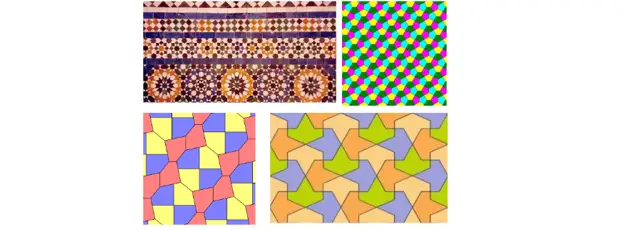
Autres pavages possibles
Mais vous avez réfléchi à la grande variété de pavages que vous avez présentés, ils ont tous quelque chose en commun, c'est-à-dire qu'ils sont périodiques. Le terme périodique fait référence au fait qu'il existe une traduction, autre que zéro, qui laisse toute la mosaïque identique. D'après ce que nous comprenons, cela équivaut au fait que si nous carrelons une surface, céramique les yeux et que quelqu'un déplace toute la mosaïque dans une direction spécifique, puis recouvre à nouveau les yeux, nous serons incapables d'apprécier la différence entre la mosaïque d'origine et le déplacé.
mosaïques sans journaux
Contrairement aux pavages périodiques, nous trouvons des pavages non périodiques, qui sont ceux pour lesquels il n'y a pas de translation, pas nulle, qui laisse la mosaïque avec le même aspect. Il n'est pas difficile de trouver des mosaïques non périodiques, il suffit, par exemple, de prendre un pavage périodique, pensons, par exemple, formé uniquement de carrés, et un seul carré de toute la mosaïque est divisé en deux triangles . De toute évidence, il s'agit toujours d'une mosaïque du plan, mais il n'y aura pas de translation qui laissera les tesselles entières identiques puisque nous pourrons faire la distinction entre la mosaïque d'origine et sa mosaïque déplacée simplement en observant la position modifiée du deux triangles.
carrelage apériodique
Mais c'est maintenant que les choses deviennent intéressantes, car c'est quand le concept de mosaïque apériodique apparaît, qui sont ceux qui, tout en n'étant pas périodiques, satisfont à la condition supplémentaire qu'ils n'ont pas de régions périodiques arbitrairement grandes. De la même manière cette idée peut être entendue comme dans une mosaïque apériodique, si on prend un morceau assez grand, elle ne se répète pas dans le reste de la mosaïque. Assurez-vous que l'échantillon de mosaïque qu'aucun périodique ne décrit auparavant n'est pas apériodique puisque nous pouvons trouver des régions arbitrairement grandes qui sont périodiques, prenez simplement des morceaux arbitrairement grands qui n'incluent aucun triangle.
Alors, la question qui se pose naturellement est la suivante :
Existe-t-il des mosaïques apériodiques ?
Cette question, qui a commencé à être étudiée dans la seconde moitié du siècle dernier, a rapidement reçu une réponse affirmative et l'un des premiers à trouver une tessellation apériodique fut Raphael M. Robinson. La mosaïque décrite par Robinson en 1971 était composée de 6 tesselles successives.

tuiles robinson
Quelques années plus tard, également dans les années 70, Roger Penrose obtient deux tuiles apériodiques qui peuvent être construites, chacune utilisant seulement deux tuiles différentes. Le premier de ces pavages est formé de deux losanges différents :
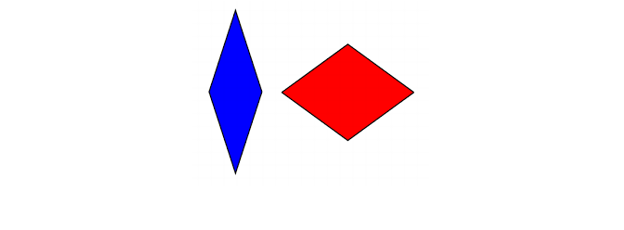
Tuiles de Penrose (losanges)
Vous pouvez produire des mosaïques telles que :
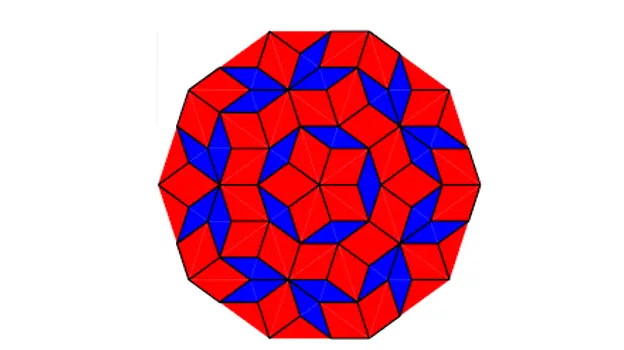
Carrelage Penrose
Le second de ces pavages apériodiques est donné par deux pièces dites cerf-volant et flèche, pour des raisons évidentes :
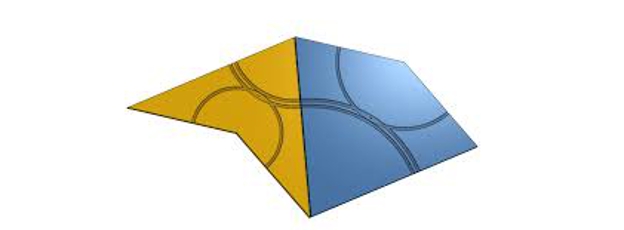
Tuiles de Penrose (comète et flèche)
Eh bien, il y a le doute qu'un plantaire pourrait être le suivant:
Existe-t-il des mosaïques apériodiques formées d'un seul carreau ?
Ce problème est connu sous le nom de problème d'Ein Stein (de l'allemand pour "une pierre") et pendant près de 50 ans, il est resté non résolu. Jusqu'en mars dernier !
La découverte de l'Ein Stein
Le 20 mars, les scientifiques David Smith, Joseph Samuel Myers, Craig S. Kaplan et Chaim Goodman-Strauss des universités de Cambridge, Waterloo et Arkansas ont publié l'ouvrage "An aperiodic monotile" dans lequel ils décrivent une forme possible de l'un très recherché après tesselles qui donne naissance à une mosaïque apériodique avec une pièce unique.
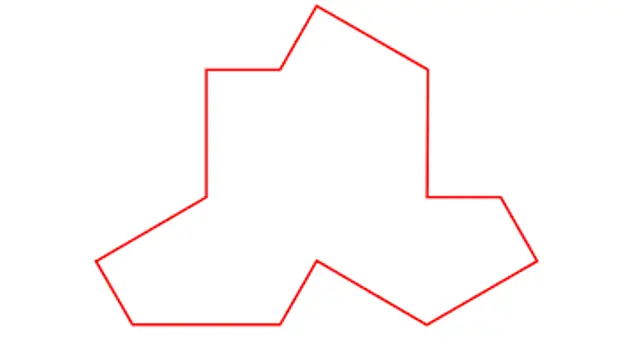
Tuile décrite par Smith, Myers, Kaplan et Goodman-Strauss
Avec cette tuile unique, qui me semble très similaire à un T-shirt, il montre que des mosaïques apériodiques comme celles-ci peuvent être construites :

Mosaïque apériodique d'une tuile
Si votre curiosité est sobre sur le sujet, vous pouvez approfondir cette découverte dans la vidéo suivante,
dans lequel ses découvreurs discutent avec d'autres personnalités de la région, dont le prix Nobel de physique Roger Penrose.
L'ABCdario de las Matemáticas est une section née de la collaboration avec la Commission de diffusion de la Société royale espagnole de mathématiques (RSME).
A PROPOS DE L'AUTEUR
Victor M. Manero
