– Lopeta etsintä! Löysimme sen vihdoinkin", komissaari MacCarnigan huudahti.
– Kuka herra? kysyi yliluutnantti Pierron.
”Yhdelle liukkaimmista roistoista, jonka voit koskaan kuvitella. Olen etsinyt sitä melkein 50 vuotta.
– Minulla ei ollut aavistustakaan, arvoisa komission jäsen. Kenestä on kyse?
– Hänen numeronsa on Ein Stein ja sen löytäminen on kestänyt melkein koko elämän.
- Kenestä on kyse? Onko sinulla kuvia sinusta siellä?
– Kyllä, minulla on se täällä, tältä se näyttää, mutta älkää antako sen viattoman ulkonäön hämätä, tämä herrasmies täällä on pitänyt meidät jännityksessä lähes kymmenen vuosikymmentä.
Joten MacCarnigan näytti agentti Pierronille kuvan Ein Steinistä, tämä kuva:
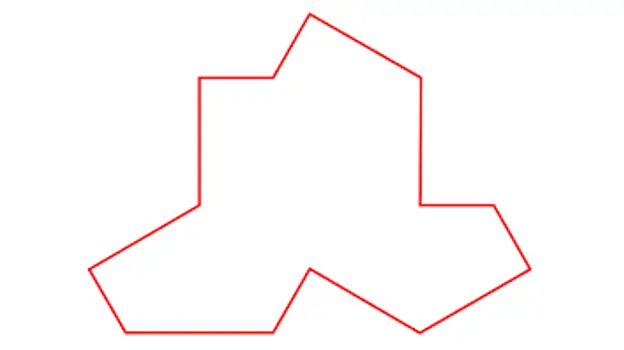
Steinissä.
Tämä lyhyt poliisien historia saattaa tuntua vitsiltä, mutta jos vaihdamme etsivät matemaatikoiksi, siitä tulee yksi upeimmista matemaattisista löydöistä, joita viime vuosina on tapahtunut. Mutta ymmärtääksemme tämän tarinan laajuuden, meidän on ensin puhuttava yhdestä matematiikan ja taiteen sulautumisesta: mosaiikit.
mosaiikkilehdet
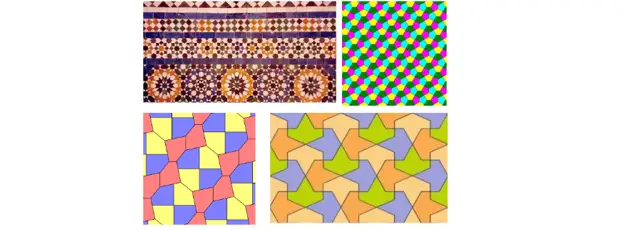
Olemme kaikki nähneet mosaiikin jossain vaiheessa elämäämme. Nämä ovat pieniä taiteellisia tai koristeellisia teoksia, jotka on tehty pienistä toisiinsa sopivista kappaleista.


Muutamia esimerkkejä mosaiikeista
Kun puhumme matematiikan mosaiikeista, tarkoitamme yleensä niin kutsuttuja tessellaatioita, jotka ovat tapa järjestää kappaleita tai laattoja siten, että niillä on yhteiset reunat eivätkä ne jätä reikiä.
Kauan sitten matemaatikot ja matematiikka esittivät seuraavan kysymyksen
Millaisilla palasilla koneen voi laatoittaa?
Eli minkä tyyppisiä paloja voin käyttää siihen, asettamalla ne niin, että laatat koskettavat toisiaan yhteisillä puolilla, tasossa ei ole rakoja. Ympyrät eivät selvästikään kuulu tähän valintaryhmään, koska jos haluan laatoittaa tason käyttämällä vain ympyröitä, minulle jää reikiä. Tule, minun on valettava kiinteä laasti.

ympyrät jättävät aukkoja
On kuitenkin olemassa monia muita muotoja, joilla voimme laatoittaa tason, kuten kolmioita, neliöitä tai kuusikulmioita.

Tessellaatio yhdellä säännöllisellä polygonilla
Tai voimme laatoittaa tason näiden tai muiden hahmojen yhdistelmillä.

Tessellaatio useilla säännöllisillä polygoneilla
Tai voit jopa laatoittaa koneen ylellisillä yhdistelmillä:
Muut mahdolliset laatoitukset
Mutta olet pohtinut esittämääsi suurta valikoimaa laatoitusta, niillä kaikilla on jotain yhteistä, eli se, että ne ovat säännöllisiä. Termi jaksollinen viittaa siihen, että on jokin muu käännös kuin nolla, joka jättää koko mosaiikin ennalleen. Ymmärryksessämme se vastaa sitä tosiasiaa, että jos laatoimme pinnan, keraamistamme silmät ja joku siirtää koko mosaiikin tiettyyn suuntaan ja peittää sitten silmät uudelleen, emme pysty ymmärtämään alkuperäisen mosaiikin eroa. ja siirtymään joutunut.
mosaiikit ilman sanomalehtiä
Toisin kuin jaksottaiset laatoitukset, löydämme ei-jaksolliset laatoitukset, jotka ovat sellaisia, joille ei ole käännöstä, ei nollaa, joka jättää mosaiikin samanlaisena. Ei-jaksollisten mosaiikien löytäminen ei ole vaikeaa, riittää esimerkiksi jaksollinen laatoitus, ajatellaan esimerkiksi vain neliöistä muodostettua, ja koko mosaiikin yksittäinen neliö on jaettu kahteen kolmioon . On selvää, että se on edelleen tason tessellaatio, mutta ei tule olemaan mitään käännöstä, joka jättäisi kaikki tesseraat ennalleen, koska pystymme erottamaan alkuperäisen mosaiikin ja sen siirretyn mosaiikin yksinkertaisesti tarkkailemalla mosaiikin muutettua sijaintia. kaksi kolmiota.
jaksollinen laatoitus
Mutta nyt asiat muuttuvat mielenkiintoisiksi, koska silloin ilmaantuu käsite jaksoittaisesta mosaiikkista, jotka ovat sellaisia, jotka eivät ole jaksollisia, mutta täyttävät sen lisäehdon, että niillä ei ole mielivaltaisen suuria alueita, jotka ovat jaksollisia. Samalla tavalla tämä ajatus kuuluu kuin jaksollisessa mosaiikissa, jos otamme riittävän ison palan, se ei toistu mosaiikin muussa osassa. Varmista, että mosaiikkinäyte, jota mikään aikakauslehti ei kuvaa aiemmin, ei ole aperiodinen, koska voimme löytää mielivaltaisen suuria alueita, jotka ovat jaksollisia, ota vain mielivaltaisen suuria paloja, jotka eivät sisällä kumpaakaan kolmiota.
Joten luonnollisesti herää kysymys:
Onko olemassa jaksollisia mosaiikkeja?
Tämä kysymys, jota alettiin tutkia viime vuosisadan toisella puoliskolla, sai pian myöntävän vastauksen, ja yksi ensimmäisistä, jotka löysivät aperiodisen tessellaation, oli Raphael M. Robinson. Robinsonin vuonna 1971 kuvaama mosaiikki koostui kuudesta peräkkäisestä tesserasta.

robinson laatat
Muutamaa vuotta myöhemmin, myös 70-luvulla, Roger Penrose sai kaksi jaksollista laattaa, jotka voitiin rakentaa, joista jokaisessa käytettiin vain kahta erilaista laattaa. Ensimmäinen näistä tessellaatioista muodostuu kahdesta erilaisesta rombista:
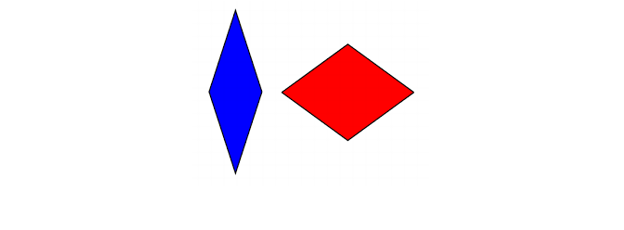
Penrose-laatat (rombit)
Voit valmistaa mosaiikit sellaisina:
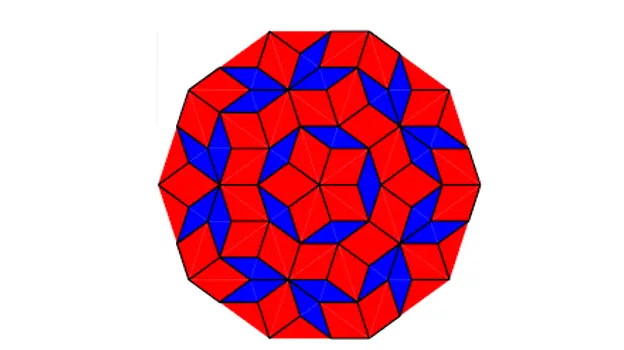
Penrose laatoitus
Toinen näistä jaksollisista laatoista saadaan kahdella kappaleella, jotka tunnetaan nimellä leija ja nuoli, ilmeisistä syistä:
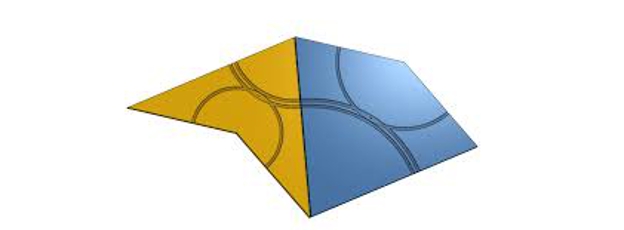
Penrose-laatat (komeetta ja nuoli)
No, on epäilystä siitä, että plantaari voisi olla seuraava:
Onko olemassa yksittäisen laatan muodostamia jaksollisia mosaiikkeja?
Tämä ongelma on tunnettu Ein Stein -ongelmana (saksan kielestä "kivi"), ja se on ollut ratkaisematta lähes 50 vuoden ajan. Viime maaliskuuhun asti!
Ein Steinin löytö
Tiedemiehet David Smith, Joseph Samuel Myers, Craig S. Kaplan ja Chaim Goodman-Strauss Cambridgen, Waterloon ja Arkansasin yliopistoista julkaisivat 20. maaliskuuta teoksen "An aperidic monotile", jossa he kuvasivat erästä mahdollista muotoa tesseraen jälkeen, joka synnyttää jaksollisen mosaiikin ainutlaatuisella kappaleella.
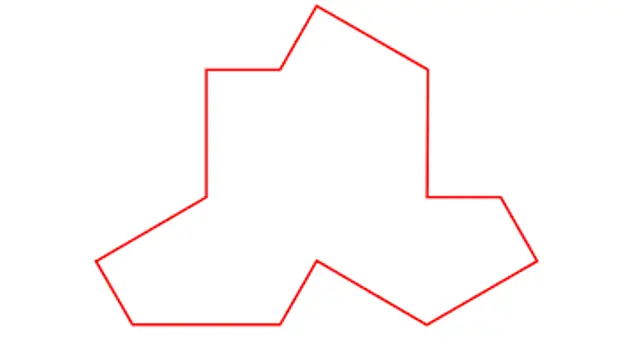
Smithin, Myersin, Kaplanin ja Goodman-Straussin kuvaama laatta
Tällä yksittäisellä laatalla, joka näyttää minusta hyvin samanlaiselta kuin T-paita, hän osoittaa, että seuraavanlaisia jaksollisia mosaiikkeja voidaan rakentaa:

Ajoittainen laatan mosaiikki
Jos uteliaisuutesi on raittiita aiheesta, voit syventää tätä löytöä seuraavassa videossa,
jossa sen löytäjät puhuvat muiden asiaankuuluvien ihmisten kanssa alueella, mukaan lukien fysiikan Nobelin Roger Penrosen kanssa.
ABCdario de las Matemáticas on osa, joka syntyy yhteistyöstä Espanjan kuninkaallisen matematiikan seuran (RSME) levityskomission kanssa.
KIRJAILIJASTA
Victor M. Manero

