– Stop eftersøgningen! Vi har endelig fundet det, udbrød kommissær MacCarnigan.
– Hvem sir? spurgte sekondløjtnant Pierron.
"Til en af de mest glatte slyngler, du nogensinde kunne forestille dig. Jeg har ledt efter den i næsten 50 år.
– Jeg anede ikke, hr. kommissær. Hvem handler det om?
– Hans nummer er Ein Stein, og det har taget mig næsten et helt liv at finde det.
- Hvem handler det om? Har du billeder af dig derude?
– Ja, jeg har det lige her, sådan ser det ud, men lad dig ikke snyde af dets uskyldige udseende, denne herre her har holdt os i spænding i næsten ti årtier.
Så MacCarnigan viste agent Pierron billedet af Ein Stein, dette billede:
I Stein.
Denne korte historie om politifolk kan virke som en joke, men hvis vi skifter detektiver til matematikere, bliver det en af de mest vidunderlige matematiske opdagelser, der er sket i de senere år. Men for at forstå rækkevidden af denne historie, må vi først tale om et af de felter, hvor matematik og kunst smelter sammen: mosaikker.
mosaikaviser
Vi har alle set en mosaik på et tidspunkt i vores liv. Det er små kunstneriske eller dekorative værker, der er lavet ved hjælp af små stykker, der passer sammen.


Nogle eksempler på mosaikker
Når vi taler om mosaikker i matematik, refererer vi normalt til det, der er kendt som tesseller, som er en måde at arrangere brikker eller fliser på, så disse brikker har fælles kanter og ikke efterlader huller.
For lang tid siden rejste matematikere og matematik følgende spørgsmål
Hvilken slags stykker kan jeg flisebelægge flyet med?
Det vil sige, hvilken type stykker kan jeg bruge til det, placere dem så fliserne rører hinanden på fælles sider, der er ingen huller i planen. Det er klart, at cirklerne ikke er i denne udvalgte gruppe, da hvis jeg ønsker at flisebelægge flyet med kun cirkler, vil de efterlade mig med huller. Kom nu, jeg bliver nødt til at støbe fast fugemasse.

cirkler efterlader huller
Der er dog mange andre former, som vi kan flisebelægge planet med, såsom trekanter, firkanter eller sekskanter.

Tessellation med en enkelt regulær polygon
Eller vi kan flisebelægge flyet med kombinationer af disse eller andre figurer.

Tessellation med flere regulære polygoner
Eller du kan endda flisebelægge flyet med mere ekstravagante kombinationer:
Andre mulige fliser
Men du har tænkt over den store variation af flisebelægninger, som du har præsenteret, de har alle noget tilfælles, og det vil sige, at de er periodiske. Udtrykket periodisk refererer til det faktum, at der er en anden oversættelse end nul, der efterlader hele mosaikken den samme. Efter hvad vi forstår, svarer det til, at hvis vi fliser en overflade, keramikerer øjnene og nogen flytter hele mosaikken i en bestemt retning og derefter dækker øjnene igen, vil vi ikke være i stand til at forstå forskellen mellem den originale mosaik og den forskudte.
mosaikker uden aviser
I modsætning til periodiske flisebelægninger finder vi ikke-periodiske flisebelægninger, som er dem, for hvilke der ikke er nogen oversættelse, ikke nul, der efterlader mosaikken med samme udseende. Det er ikke svært at finde ikke-periodiske mosaikker, det er nok, for eksempel at tage en periodisk flisebelægning, lad os for eksempel tænke på en, der kun er dannet af firkanter, og en enkelt firkant af hele mosaikken er opdelt i to trekanter. Det er klart, at det stadig er en tessellation af flyet, men der vil ikke være nogen oversættelse, der vil efterlade hele tessærerne det samme, da vi vil være i stand til at skelne mellem den originale mosaik og dens forskudte blot ved at observere den modificerede position af de to trekanter.
aperiodisk flisebelægning
Men det er nu, tingene bliver interessante, for det er, når begrebet aperiodisk mosaik dukker op, som er dem, der, selvom de ikke er periodiske, opfylder den ekstra betingelse, at de ikke har vilkårligt store områder, der er periodiske. På samme måde kan denne idé høres som i en aperiodisk mosaik, hvis vi tager et stort nok stykke, gentages det ikke i resten af mosaikken. Sørg for, at mosaikprøven, som intet tidsskrift tidligere beskriver, ikke er aperiodisk, da vi kan finde vilkårligt store områder, der er periodiske, tag blot vilkårligt store stykker, der ikke inkluderer nogen af trekanter.
Så spørgsmålet, der naturligt opstår, er følgende:
Er der aperiodiske mosaikker?
Dette spørgsmål, som begyndte at blive undersøgt i anden halvdel af forrige århundrede, fik snart et bekræftende svar, og en af de første til at finde en aperiodisk tessellation var Raphael M. Robinson. Mosaikken beskrevet af Robinson i 1971 bestod af 6 på hinanden følgende tessærer.

robinson fliser
Et par år senere, også i 70'erne, opnåede Roger Penrose to aperiodiske fliser, der kunne bygges, hver med kun to forskellige fliser. Den første af disse tesseller er dannet af to forskellige rhombuses:
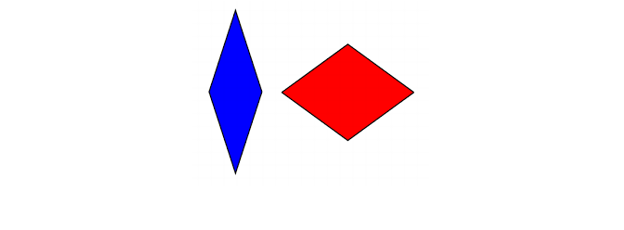
Penrose fliser (rhombuses)
Du kan fremstille mosaikker som sådan:
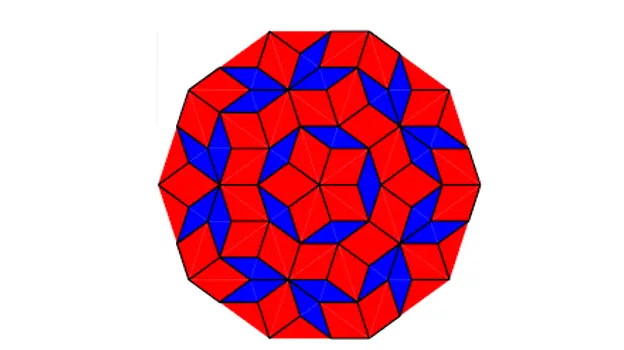
Penrose flisebelægning
Den anden af disse aperiodiske fliser er givet af to stykker kendt som drage og pil, af indlysende årsager:
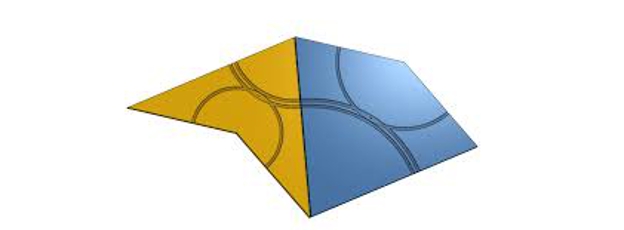
Penrose fliser (komet og pil)
Nå, der er tvivl om, at en plantar kan være følgende:
Er der aperiodiske mosaikker dannet af en enkelt flise?
Dette problem har været kendt som Ein Stein-problemet (fra tysk for "en sten") og i næsten 50 år har det været uløst. Indtil sidste marts!
Opdagelsen af Ein Stein
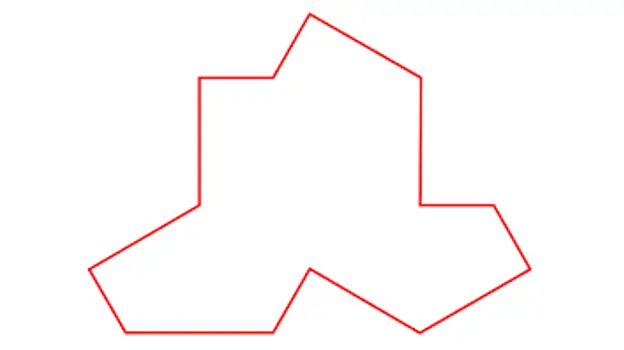
Den 20. marts udgav videnskabsmændene David Smith, Joseph Samuel Myers, Craig S. Kaplan og Chaim Goodman-Strauss fra universiteterne i Cambridge, Waterloo og Arkansas værket 'An aperiodic monotile', hvori de beskrev en mulig form på den meget eftertragtede flise, der giver anledning til en aperiodisk mosaik med et enkelt stykke.
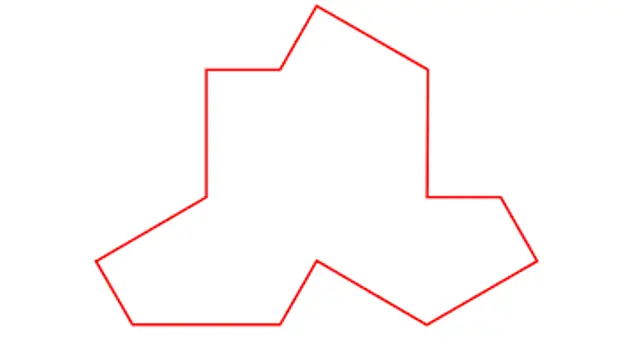
Tile beskrevet af Smith, Myers, Kaplan og Goodman-Strauss
Med denne enkelt flise, som for mig forekommer at ligne en T-shirt, viser han, at der kan bygges aperiodiske mosaikker som følgende:

Aperiodisk mosaik af en flise
Hvis din nysgerrighed er ædru på emnet, kan du dykke dybere ned i denne opdagelse i den følgende video,
hvor dens opdagere taler med andre relevante personer i området, herunder Nobelprisen i fysik Roger Penrose.
ABCdario de las Matemáticas er en sektion, der udspringer af samarbejdet med Formidlingskommissionen for Royal Spanish Mathematical Society (RSME).
OM FORFATTEREN
Victor M. Manero

