– Спрете търсенето! Най-накрая го открихме — възкликна комисар МакКарниган.
– Кой господин? — попита втори лейтенант Пиерън.
„На един от най-хлъзгавите мошеници, които можете да си представите. Търся го почти 50 години.
– Нямах представа, г-н комисар. за кого става въпрос
– Номерът му е Ein Stein и ми отне почти цял живот да го намеря.
- За кого става въпрос? Имаш ли твои снимки там?
– Да, имам го точно тук, така изглежда, но не се заблуждавайте от невинния му вид, този господин тук ни държи в напрежение почти десет десетилетия.
И така, MacCarnigan показа на агент Pierron снимката на Ein Stein, тази снимка:
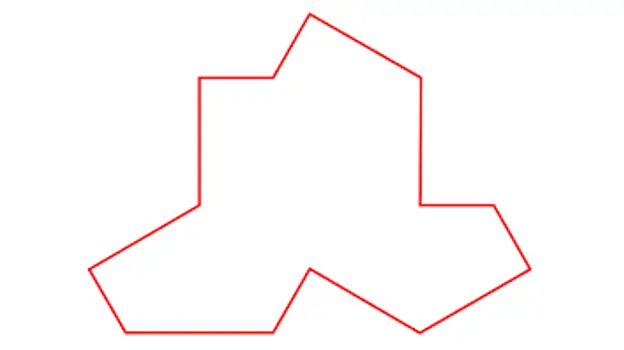
В Щайн.
Тази кратка история на полицаите може да изглежда като шега, но ако сменим детективите с математици, това се превръща в едно от най-прекрасните математически открития, случвали се през последните години. Но за да разберем обхвата на тази история, първо трябва да говорим за една от областите, в които математиката и изкуството се сливат: мозайките.
мозаечни вестници
Всички сме виждали мозайка в някакъв момент от живота си. Това са малки художествени или декоративни произведения, които са направени с помощта на малки парчета, които пасват заедно.


Някои примери за мозайки
Когато говорим за мозайки в математиката, обикновено говорим за това, което е известно като теселации, което е начин за подреждане на парчета или плочки, така че тези парчета да имат общи ръбове и да не оставят дупки.
Преди много време математиците и математиците повдигнаха следния въпрос
С какви парчета мога да облицовам самолета?
Тоест, какъв тип парчета мога да използвам за това, като ги поставя така, че плочките да се допират една до друга от общи страни, да няма пропуски в плана. Ясно е, че кръговете не са в тази избрана група, тъй като ако искам да подредя равнината само с кръгове, те ще ме оставят с дупки. Хайде, ще трябва да лея фиксирана фугираща смес.

кръговете оставят празнини
Има обаче много други форми, с които можем да облицоваме самолета, като триъгълници, квадрати или шестоъгълници.

Теселация с един правилен многоъгълник
Или можем да облицоваме самолета с комбинации от тези или други фигури.

Теселация с няколко правилни полигона
Или дори можете да облицовате самолета с по-екстравагантни комбинации:
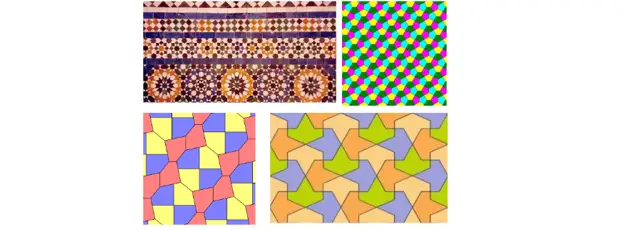
Други възможни облицовки
Но вие се замислихте върху голямото разнообразие от подложки, които представихте, всички те имат нещо общо, а именно, че са периодични. Терминът периодичен се отнася до факта, че има някакъв превод, различен от нула, който оставя цялата мозайка същата. От това, което разбираме, това е еквивалентно на факта, че ако облицоваме повърхност, облицоваме очите с керамика и някой премести цялата мозайка в определена посока и след това отново покрие очите, няма да можем да оценим разликата между оригиналната мозайка и изместеният.
мозайки без вестници
За разлика от периодичните подреждания намираме непериодични подреждания, които са тези, за които няма превод, а не нула, което оставя мозайката със същия вид. Не е трудно да се намерят непериодични мозайки, достатъчно е, например, да се вземе периодична облицовка, нека помислим, например, че е образувана само от квадрати, а един квадрат от цялата мозайка е разделен на два триъгълника . Ясно е, че това все още е мозайка на равнината, но няма да има превод, който да остави цялата тесера същата, тъй като ще можем да направим разлика между оригиналната мозайка и нейната изместена, просто като наблюдаваме модифицираната позиция на два триъгълника.
апериодично облицоване
Но сега е моментът, в който нещата стават интересни, защото тогава се появява концепцията за апериодични мозайки, които са тези, които, въпреки че не са периодични, отговарят на допълнителното условие, че нямат произволно големи области, които са периодични. По същия начин тази идея може да се чуе като в апериодична мозайка, ако вземем достатъчно голямо парче, то не се повтаря в останалата част от мозайката. Уверете се, че мозаечната проба, която нито едно периодично издание не описва преди, не е апериодична, тъй като можем да намерим произволно големи области, които са периодични, просто вземете произволно големи парчета, които не включват нито един от триъгълниците.
И така, въпросът, който естествено възниква, е следният:
Има ли апериодични мозайки?
Този въпрос, който започна да се изучава през втората половина на миналия век, скоро получи утвърдителен отговор и един от първите, които откриха апериодична теселация, беше Рафаел М. Робинсън. Мозайката, описана от Робинсън през 1971 г., се състои от 6 последователни тесери.

Робинзон плочки
Няколко години по-късно, също през 70-те години на миналия век, Роджър Пенроуз получава две апериодични плочки, които могат да бъдат построени, като всяка използва само две различни плочки. Първата от тези теселации е образувана от два различни ромба:
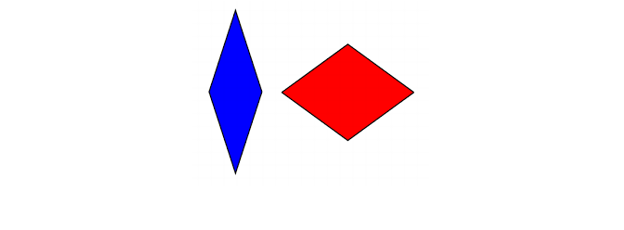
Плочки на Пенроуз (ромби)
Можете да произвеждате мозайки като такива:
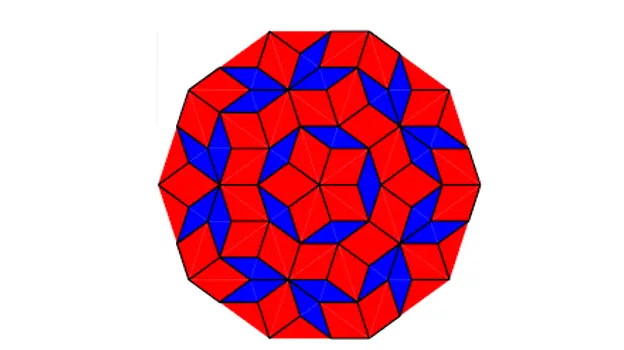
Облицовка на Пенроуз
Второто от тези апериодични плочки се дава от две части, известни като хвърчило и стрела, по очевидни причини:
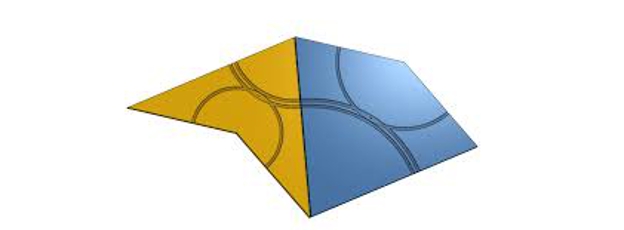
Плочки на Пенроуз (комета и стрела)
Е, има съмнение, че плантарната може да бъде следната:
Има ли апериодични мозайки, образувани от една плочка?
Този проблем е известен като проблемът на Айн Щайн (от немски за "камък") и почти 50 години остава нерешен. До миналия март!
Откриването на Айн Щайн
На 20 март учените Дейвид Смит, Джоузеф Самуел Майерс, Крейг С. Каплан и Хаим Гудман-Щраус от университетите в Кеймбридж, Ватерло и Арканзас публикуваха работата „Апериодичен монотил“, в която описаха възможна форма на много търсения след тесери, което води до апериодична мозайка с уникално парче.
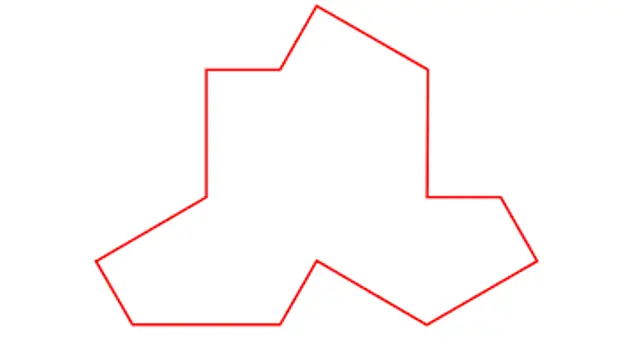
Плочка, описана от Смит, Майерс, Каплан и Гудман-Щраус
С тази единична плочка, която ми се струва много подобна на тениска, той показва, че могат да се изградят апериодични мозайки като следните:

Апериодична мозайка от плочки
Ако любопитството ви е трезво по темата, можете да се задълбочите в това откритие в следния видеоклип,
в който неговите откриватели разговарят с други подходящи хора в района, включително носителя на Нобелова награда по физика Роджър Пенроуз.
ABCdario de las Matemáticas е раздел, който възниква от сътрудничеството с Комисията за разпространение на Кралското испанско математическо дружество (RSME).
ЗА АВТОРА
Виктор М. Манеро

